
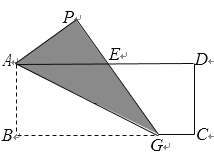
【题目】如图,矩形纸片ABCD中,AB=4,BC=10,G是BC边上一点,沿AG折叠△ABG,点B的落点为P,GP交AD于点E. 若E是AD的中点,则BG的长是_______.
科目:初中数学 来源: 题型:
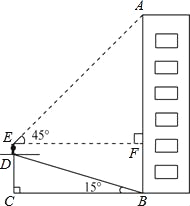
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
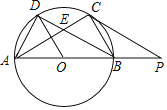
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
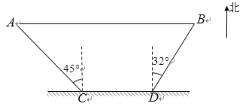
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
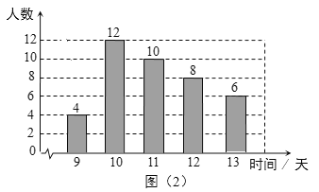
【题目】学校为了解全校学生参加社会实践活动情况,随机调查了部分学生一学期参加社会实践活动的时间(单位:天),并用得到的数据绘制了统计图(1)和图 (2). 请根据图中提供的信息,回答下列问题:

![]()
(1) 本次随机调查的学生人数是_______,图(1)中m的值是_______;
(2)求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数;
(3)该校有480名学生,根据获取的社会实践活动时间样本数据,估计该校一学期社会实践活动时间大于10 天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
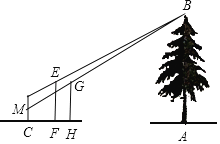
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com