
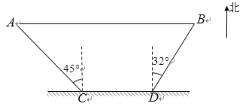
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.
【答案】115 m
【解析】
过C作CH⊥AB于点H,过点D作DG⊥AB于点G,可得四边形CHGD是矩形,根据解直角三角形中特殊角的三角函数值可求得AH和BG长,即可求得AB长.
解:如图,过C作CH⊥AB于点H,过点D作DG⊥AB于点G,

∵AB∥CD,∴可得CH∥DG.
∴四边形CHGD是矩形.
∴ CH=DG,HG=CD.
在Rt△ACH中,∠ACH=45°,AC=60,
∴CH=AC·cos45°=60×![]() =
=![]() ,
,
AH=AC·sin45°=60×![]() =
=![]() .
.
在Rt△BDG中,∠DBG=32°,DG=CH=![]() ,
,
∴BG= DG·tan32° =![]() ×tan32°.
×tan32°.
∴ AB=AH+HG+BG ≈![]() +46+
+46+![]() ×0.62 ≈ 115.
×0.62 ≈ 115.
答:栈道AB的长度约为115 m.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
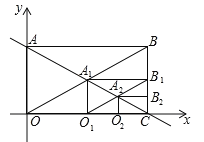
【题目】如图,直线y=﹣![]() x+2与x轴y轴分别交于A、C两点,以AC为对角线作第一个矩形ABCO,对角线交点为A1,再以CA1为对角线作第二个矩形A1B1CO1,对角线交点为A2,同法作第三个矩形A2B2CO2对角线交点为A3,…以此类推,则第2020个矩形对角线交点A2020的坐标为_____.
x+2与x轴y轴分别交于A、C两点,以AC为对角线作第一个矩形ABCO,对角线交点为A1,再以CA1为对角线作第二个矩形A1B1CO1,对角线交点为A2,同法作第三个矩形A2B2CO2对角线交点为A3,…以此类推,则第2020个矩形对角线交点A2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
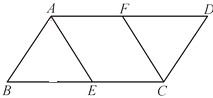
【题目】如图,在ABCD中,BC=2AB=4,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
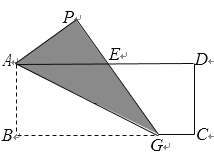
【题目】如图,矩形纸片ABCD中,AB=4,BC=10,G是BC边上一点,沿AG折叠△ABG,点B的落点为P,GP交AD于点E. 若E是AD的中点,则BG的长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=10,G是BC边上一点,沿AG折叠△ABG,点B的落点为P,GP交AD于点E. 若E是AD的中点,则BG的长是_______.
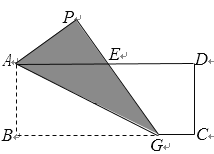
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() (
(![]() )与
)与![]() 轴交于A、B两点(点B在A的右侧),与
轴交于A、B两点(点B在A的右侧),与![]() 轴交于点C,D是抛物线的顶点.
轴交于点C,D是抛物线的顶点.
(1)当![]() 时,求顶点D 的坐标
时,求顶点D 的坐标
(2)若OD = OB,求![]() 的值;
的值;
(3)设E为A,B两点间抛物线上的一个动点(含端点A,B),过点E作EH⊥![]() 轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为
轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
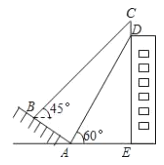
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.
(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.
(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m.参考数据:![]() ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com