
【题目】在平面直角坐标系中,抛物线![]() (
(![]() )与
)与![]() 轴交于A、B两点(点B在A的右侧),与
轴交于A、B两点(点B在A的右侧),与![]() 轴交于点C,D是抛物线的顶点.
轴交于点C,D是抛物线的顶点.
(1)当![]() 时,求顶点D 的坐标
时,求顶点D 的坐标
(2)若OD = OB,求![]() 的值;
的值;
(3)设E为A,B两点间抛物线上的一个动点(含端点A,B),过点E作EH⊥![]() 轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为
轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)D(1,4);(2)![]() ;(3)
;(3)![]()
【解析】
(1)把![]() 代入解析式可求出解析式,再把解析式化为顶点式即可求得结果.
代入解析式可求出解析式,再把解析式化为顶点式即可求得结果.
(2)令y=0可得出![]() ,
,![]() ,即可得到A,B的坐标,再把一般式化为顶点式可得到顶点坐标D,根据勾股定理可得
,即可得到A,B的坐标,再把一般式化为顶点式可得到顶点坐标D,根据勾股定理可得![]() ,再根据OD = OB列出等式即可求出结果.
,再根据OD = OB列出等式即可求出结果.
(3)设经过点B,C 的直线为![]() 把点代入可得到
把点代入可得到![]() ,再设点E(
,再设点E(![]() ,
,![]() )在抛物线
)在抛物线![]() (
(![]() )上,可得点F(
)上,可得点F(![]() ,
,![]() ), 根据A(
), 根据A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),点E 在点A,B间的抛物线上,知道线段EF的长有两种情况,分别是当
),点E 在点A,B间的抛物线上,知道线段EF的长有两种情况,分别是当 ![]() 时和当
时和当 ![]() 时,即可求出结果.
时,即可求出结果.
(1)解:∵ ![]() ,∴
,∴ ![]() .
.
由![]() ,
,
∴ 顶点D(1,4).
(2)解:当![]() 时,有
时,有![]() ,即
,即![]() ,
,
解得![]() ,
,![]() .
.
∴ A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ).
).
∴ OB =3.
∵ ![]() .
.
∴ D(![]() ,
,![]() ).
).
根据勾股定理,有![]() .
.
∵ OD=OB,∴ ![]() .
.
解得 ![]() ,
,![]() (舍),
(舍),
∴ ![]() .
.
(3)解:设经过点B,C 的直线为![]() .
.
把点 B(![]() ,
,![]() ),C(
),C(![]() ,
,![]() )代入,得
)代入,得![]() .
.
设点E(![]() ,
,![]() )在抛物线
)在抛物线![]() (
(![]() )上,
)上,
有![]() ,点F(
,点F(![]() ,
,![]() ).
).
∵ A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),点E 在点A,B间的抛物线上.
),点E 在点A,B间的抛物线上.
∴ 线段EF的长有两种情况:
①当 ![]() 时,
时,
∴ EF =t =![]() .
.
∵ ![]() ,
,![]() ,
,
∴ ![]() 有最大值.
有最大值.
即 当![]() 时,t的最大值是
时,t的最大值是![]() .
.
②当 ![]() 时,
时,
∴ EF =t =![]() .
.
∵ ![]() ,
,![]()
∴ 当 ![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
∴ 当![]() 时,
时,![]() 的值最大,最大值是
的值最大,最大值是![]() .
.
∵ ![]() ,∴
,∴![]() .
.
![]() 时,
时,![]() 的最大值是
的最大值是![]() .
.
∴ ![]() . 即
. 即![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
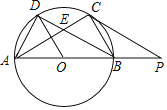
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
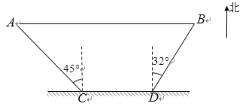
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
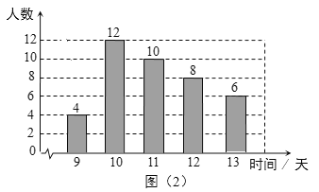
【题目】学校为了解全校学生参加社会实践活动情况,随机调查了部分学生一学期参加社会实践活动的时间(单位:天),并用得到的数据绘制了统计图(1)和图 (2). 请根据图中提供的信息,回答下列问题:

![]()
(1) 本次随机调查的学生人数是_______,图(1)中m的值是_______;
(2)求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数;
(3)该校有480名学生,根据获取的社会实践活动时间样本数据,估计该校一学期社会实践活动时间大于10 天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
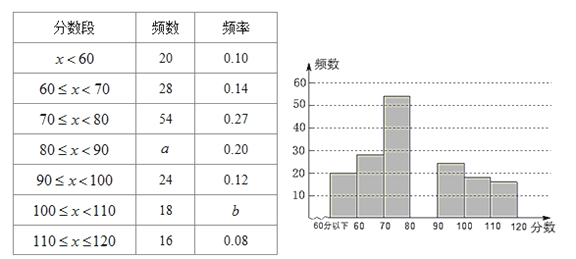
请根据以上图表提供的信息,解答下列问题:
(1)随机抽取部分学生的总人数是_________人,表格中的![]() _________.
_________.
(2)请补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市16000名九年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
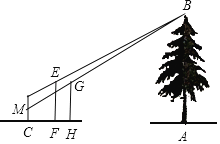
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年由于受“疫情”影响,某厂只能按用户的月需求量![]() (件)(
(件)(![]() )完成一种产品的生产,每件的售价为18万元,每件的成本
)完成一种产品的生产,每件的售价为18万元,每件的成本![]() (万元),
(万元),![]() 与
与![]() 的关系式为
的关系式为![]() (
(![]() ,
,![]() 为常数),经市场调研发现,月需求量
为常数),经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到下表中的数据.
为常数),且得到下表中的数据.

(1)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)推断哪个月产品的需求量最小?最小为多少件?
(3)在这一年12个月中,若![]() 个月和第(
个月和第(![]() )个月的利润相差最大,求
)个月的利润相差最大,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
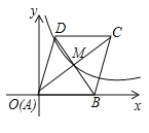
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,顶点
重合,顶点![]() 落在
落在![]() 轴的正半轴上,对角线
轴的正半轴上,对角线![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 恰好都在反比例函数
恰好都在反比例函数![]() 的图象上,若
的图象上,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com