
分析 根据规律化简即可.
解答 解:(1)∵①$\sqrt{{5^2}-{4^2}}$=$\sqrt{(5-4)×(5+4)}$=1×3;
②$\sqrt{{{17}^2}-{8^2}}$=$\sqrt{(17-8)×(17+8)}$=3×5;
③$\sqrt{{{37}^2}-{{12}^2}}$=$\sqrt{(37-12)×(37+12)}$=5×7;
…
∴$\sqrt{{65}^{2}-1{6}^{2}}$=$\sqrt{(65-16)×(65+16)}$=7×9;
故答案为:7,9;
(2)由(1)知,第n个等式$\sqrt{{{({4{n^2}+1})}^2}-16{n^2}}$=(2n-1)(2n+1),
证明如下:$\sqrt{{{({4{n^2}+1})}^2}-16{n^2}}=\sqrt{({4{n^2}-4n+1})({4{n^2}+4n+1})}=\sqrt{{{({2n-1})}^2}{{({2n+1})}^2}}=({2n-1})({2n+1})$.
点评 本题主要考查了二次根式的性质及化简,根据已知找出规律是解答此题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
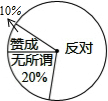 “校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°.
“校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
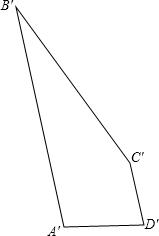 如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.
如图所示,四边形A′B′C′D′是将四边形ABCD平移后得到的,已知A′B′=13,B′C′=12,C′D′=3,D′A′=4,求四边形ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
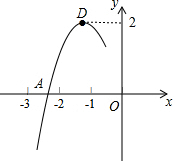 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
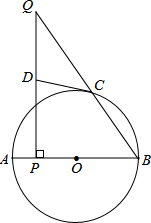 如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com