
���� ��1����7�꼶Ů��x�ˡ�����y�ˣ�����꼶Ů���У�x+24���ˡ�������1.2y�ˣ��ֱ�����ߡ����꼶�С�Ů���������г������飬�ⷽ����ɵã�
��2����45����60���ֱ�Ϊx����y�������ݣ���ͳ�һ��9����45��װ������+60װ������=ѧ������+��ʦ�������г������飻
��3���и����ʵ������������3��45����5��60��װ��435�ˣ�����4500Ԫ��
��� �⣺��7�꼶Ů��x�ˣ�����y�ˣ���
$\left\{\begin{array}{l}{x+y=180}\\{x+24+1.2y=224}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=80}\\{y=100}\end{array}\right.$��
��������100+100��1.2=220���ˣ�
Ů����80��2+24=184���ˣ���
���������ݶ�������Ů��184�ˣ�����220�ˣ�
��2����45��Ϊx����60��Ϊy������
$\left\{\begin{array}{l}{x+y=9}\\{45x+60y=180+224+31}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=7}\\{y=2}\end{array}\right.$
�������Ϊ500��7+600��2=4700��Ԫ����
��������45��7����60����ͳ�2�����������Ϊ4700Ԫ��
��3���������������
������45��3����60��5��ʱ����װ������Ϊ3��45+5��60=435���ˣ���
��ʱ�ķ���Ϊ��500��3+600��5=4500��4700��Ԫ����
���и�������������������45��3����60��5��ʱ����ø��٣�Ϊ4500Ԫ��
���� ������Ҫ�����Ԫһ�η��̵�Ӧ�ã���δ֪������������ȷ��ʾ���������Ǹ�����ȷץס��ȹ�ϵ�г������ǽ���Ĺؼ���


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
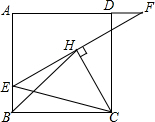 ��ͼ����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��BE=DF������EF����CH��EF������CE��BH����BH=8��EF=4$\sqrt{10}$����������ABCD�ı߳��ǣ�������
��ͼ����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��BE=DF������EF����CH��EF������CE��BH����BH=8��EF=4$\sqrt{10}$����������ABCD�ı߳��ǣ�������| A�� | 5$\sqrt{2}$ | B�� | 6$\sqrt{2}$ | C�� | 5$\sqrt{5}$ | D�� | 6$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
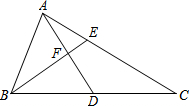 ��֪����ͼ��AD��BE�ֱ��ǡ�ABC�����ߺͽ�ƽ���ߣ�AD��BE��AD=8��BF=5����AC�ij�����13��
��֪����ͼ��AD��BE�ֱ��ǡ�ABC�����ߺͽ�ƽ���ߣ�AD��BE��AD=8��BF=5����AC�ij�����13���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com