
分析 如果设这个公共根为α,那么根据两根之和的表达式,可知方程x2+mx+3=0的两根为α、-m-α;方程x2-4x-(m-1)=0的两根为α、4-α.再根据两根之积的表达式,可知α(-m-α)=-3 ①,α(4-α)=-(m-1)②.联立①②,即可求出α、m的值.
解答 解:设这个公共根为α.
则方程x2+mx+3=0的两根为α、-m-α;方程x2-4x-(m-1)=0的两根为α、4-α,
由根与系数的关系有:α(-m-α)=3 ①,α(4-α)=-(m-1)②.
由②得 m=1-4α+α2③,
把③代入①得:α3-3α2+α+3=0,
即(α+3)(α2+1)=0,
∴α=-3.
把α=-3代入③得:m=4.
∴当m=4时,两个方程有一个公共根,这个公共根是-3.
点评 本题主要考查了公共根的定义,一元二次方程根与系数的关系及由两个二元二次方程组成的方程组的解法.高次方程组的解法在初中教材中不要求掌握,属于竞赛题型,本题有一定难度.


科目:初中数学 来源: 题型:选择题
 如图,P、Q、R是双曲线y=$\frac{k}{x}$(k<0)上的三点,过这三点分别作y轴的垂线,垂足分别是A、B、C,连OP、OQ、QR得到△POA、△QOB、△ROC,设它们的面积分别是S1、S2、S3,则S1、S2、S3大小关系是( )
如图,P、Q、R是双曲线y=$\frac{k}{x}$(k<0)上的三点,过这三点分别作y轴的垂线,垂足分别是A、B、C,连OP、OQ、QR得到△POA、△QOB、△ROC,设它们的面积分别是S1、S2、S3,则S1、S2、S3大小关系是( )| A. | S1<S2<S3 | B. | S2<S1<S3 | C. | S1<S3<S2 | D. | S1=S2=S3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数包括正整数、零和负分数 | |
| B. | -a不一定是整数 | |
| C. | -5和+(-5)互为相反数 | |
| D. | 两个有理数的和一定大于每一个加数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
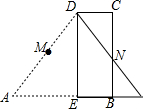 如图,设M,N分别是直角梯形ABCD两腰的中点,DE⊥AB,将△ADE沿DE翻折,M、N恰好重合,则AB:BE等于( )
如图,设M,N分别是直角梯形ABCD两腰的中点,DE⊥AB,将△ADE沿DE翻折,M、N恰好重合,则AB:BE等于( )| A. | 2:1 | B. | 1:2 | C. | 3:1 | D. | 1:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某足球运动员在离地面高度为h米的A处(点A在点O的正上方)凌空射门,足球的飞行高度y(单位:m)与飞行的水平距离x(单位:m)之间满足函数关系式y=-$\frac{1}{64}$x2+$\frac{1}{2}$x+k,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他若能将球直接射入球门,求k的取值范围.
如图,某足球运动员在离地面高度为h米的A处(点A在点O的正上方)凌空射门,足球的飞行高度y(单位:m)与飞行的水平距离x(单位:m)之间满足函数关系式y=-$\frac{1}{64}$x2+$\frac{1}{2}$x+k,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他若能将球直接射入球门,求k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com