Question

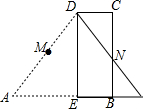
19．如图，设M，N分别是直角梯形ABCD两腰的中点，DE⊥AB，将△ADE沿DE翻折，M、N恰好重合，则AB：BE等于（　　）

• A． 2：1
• B． 1：2
• C． 3：1
• D． 1：3

Answer 1

分析 先设DE与MN交于点F，由于MN是AD、BC的中点，所以根据梯形中位线定理，可知MN∥AB，在△ADE中，MF∥AE，M是AD中点，根据平行线分线段成比例定理，可知F也是DE中点，利用三角形中位线定理，可知AE=2MF，又由于△ADE沿DE翻折，MN重合，可知MF=NF，在根据四边形FEBN是矩形，可知NF=BE，那么就可求出AB：BE的值

解答 解：设DE与MN交于点F，
∵M、N分别是AD、CB上的中点，
∴MN∥AB，
又∵M是AD的中点，
∴MF=$\frac{1}{2}$AE，
又∵M、N重合，
∴NF=BE，MF=NF，
∴AB：BE=2MF：NF=3：1，
故选：C．

点评 本题考查的是翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．