
 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 500(1-x)2=400 | B. | 400(1-x)2=500 | C. | 500(1-2x)=400 | D. | 400(1-2x)=500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
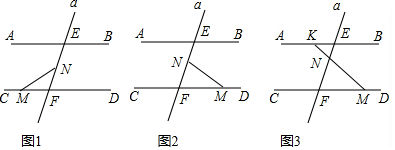
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点O是等边三角形ABC内一点,且OB=OC,将△BOC绕点C按顺时针方向旋转60°.得△ADC,连接AO、DO.
点O是等边三角形ABC内一点,且OB=OC,将△BOC绕点C按顺时针方向旋转60°.得△ADC,连接AO、DO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数包括正整数、零和负分数 | |
| B. | -a不一定是整数 | |
| C. | -5和+(-5)互为相反数 | |
| D. | 两个有理数的和一定大于每一个加数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
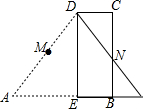 如图,设M,N分别是直角梯形ABCD两腰的中点,DE⊥AB,将△ADE沿DE翻折,M、N恰好重合,则AB:BE等于( )
如图,设M,N分别是直角梯形ABCD两腰的中点,DE⊥AB,将△ADE沿DE翻折,M、N恰好重合,则AB:BE等于( )| A. | 2:1 | B. | 1:2 | C. | 3:1 | D. | 1:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com