Question

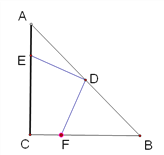
【题目】在△ABC中，∠ACB=900,AC=BC,D为AB中点.E、F分别从A、C同时出发，以每秒1个单位速度分别向C、B运动（分别到达C、B后停止运动）

（1）求证：①DE=DF；②DE⊥DF.

（2）若AB=.运动时间为t.

①求△AED面积S与t的函数关系式，并写出t的取值范围；

②若△BDF为等腰三角形，求t；

③连接EF，若EF最小，求t.

Answer 1

【答案】（1）证明见解析；（2）①；②；③t=2

【解析】试题分析：（1）连接CD，利用边角边证即可；

（2）①利用三角形的面积公式即可列出函数关系式；

②分三种情况DF=DB,DF=BF,BD=BF进行讨论即可：

③由（1）可知， 为等腰直角三角形，当DE最小（即DE⊥AC）时，EF最小，即可求解.

解：（1）连接CD，

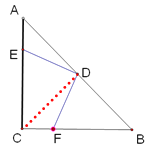
∵∠ACB=900,AC=BC,

∴△ABC是等腰直角三角形，

∴,

∵D为AB中点，

∴CD=AD=BD, ,

∴

∵E、F分别从A、C同时出发，以每秒1个单位速度分别向C、B运动，

∴

∴,

∴DE=DF, ,

∵

∴DE⊥DF.

（2）作DM⊥AC垂足为M，则DM＝,

∵AB=，且∠ACB=900,AC=BC,

∴由勾股定理得，

∴DM＝2,

∵AM=t,

∴

即

∴

②有三种情况，

当DF=BD时，此时点F在C处，即

当DF=BF时，此时点F在BC中点处，即

当DB=BF时，BF=DB= CF=即

综上所述，当△BDF为等腰三角形时， t的值为.

③当点E运动到AC中点时，EF最小，此时