
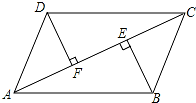
如图,AC 是▱ABCD 的一条对角线,BE⊥AC,DF⊥AC,垂足分别为 E,F.
(1)求证:△ADF≌△CBE; 求证:四边形 DFBE 是平行四边形.
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【专题】证 明题.
明题.
【分析】(1)由平行四边形的性质得出 AD∥BC,AD=BC,得出内错角相等∠DAF=∠BCE,证出
∠AFD=∠CEB=90°,由 AAS 证明△ADF≌△CBE 即可; 由(1)得:△ADF≌△CBE,由全等三角形的性质得出 DF=BE,再由 BE∥DF,即可得出四边形 DFBE 是平行四边形.
【解答】(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAF=∠BCE,
∵BE⊥AC,DF⊥AC,
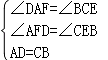 ∴BE∥DF,∠AFD=∠CEB=90°,
∴BE∥DF,∠AFD=∠CEB=90°,
在△ADF 和△CBE 中, ,
∴:△ADF≌△CBE(AAS); 解:如图所示:由(1)得:△ADF≌△CBE,
∴DF=BE,
∵BE∥DF,
∴四边形 DFBE 是平行四边形.
【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的 性质,证明三角形全 等是解决问题的关键.
等是解决问题的关键.


科目:初中数学 来源: 题型:
用反证法证明命题“钝角三角形中必有一个内角小于 45°”时,首先应该假设这个三角形中( )
A.有一个内角小于 45° B.每一个内角都小于 45°
C.有一个内角大于等于 45° D.每一个内角都大于等于 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
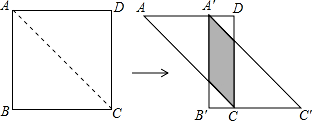
.如图,将边长为 6 的正方形 ABCD 沿其对角线 AC 剪开,再把△ABC 沿着 AD 方向平移,得到
△A′B′C′,当两个三角形重叠部分为菱形时,则 AA′为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图 1,正方形 ABCD 的边长为 4,以 AB 所在的直线为 x 轴,以 AD 所在的直线为 y 轴建立平 面直角坐标系.反比例函数 的图象与 CD 交于 E 点,与 CB 交于 F 点.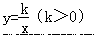
查看答案和解析>>
科目:初中数学 来源: 题型:
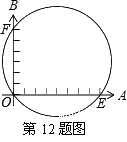
如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为
 A.10个单位
A.10个单位
B.12个单位
C.1个单位
D.15个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com