
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
【解析】
设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源:2014-2015学年江西省八年级第二次月考数学试卷(解析版) 题型:填空题
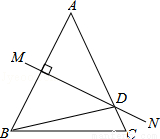
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H.
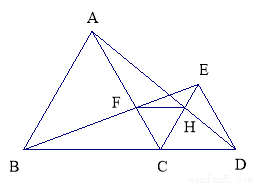
(1)证明:AB∥EC.
(2)求出∠ACE的度数.
(3)证明△ACD≌△BCE.
(4)判断△FCH为何种三角形并加以证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列图形中,一定是轴对称图形的是( )
A、三角形 B、平行四边形 C、梯形 D、圆
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省枝江市八年级12月月考数学试卷(解析版) 题型:选择题
下面说法正确的是个数有( )
①如果三角形三个内角的比是1∶2∶3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;
③若三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;
④如果∠A=∠B= ∠C,那么△ABC是直角三角形;
∠C,那么△ABC是直角三角形;
⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;
⑥在 ABC中,若∠A+∠B=∠C,则此三角形是直角三角形。
ABC中,若∠A+∠B=∠C,则此三角形是直角三角形。
A 3个 B 4个 C 5个 D 6个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省枝江市八年级12月月考数学试卷(解析版) 题型:选择题
利用基本尺规作图,下列条件中,不能作出唯一直角三角形的是( )
A.已知斜边和一锐角 B.已知一直角边和一锐角
C.已知斜边和一直角边 D.已知两个锐角
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽濉溪城关中心学校八年级上学期第三次月考数学卷(解析版) 题型:解答题
(14分)小聪和小明沿同一条路同时从学校出发到新华书店查阅资料,学校到新华书店的路程
是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达新华书店,图中折线O-A
-B-C和线段OD分别表示两人离学校的路程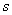 (千米)与所经过的时间
(千米)与所经过的时间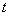 (分钟)之间的函数关系,请根
(分钟)之间的函数关系,请根
据图象回答下列问题:

(1)小聪在新华书店查阅资料的时间为________分钟,小聪返回学校的速度为_______千米/分钟.
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com