
【题目】①计算:(-1)2+ ![]() -
- ![]() -︱-5︱
-︱-5︱
②用适当的方法解方程:x2=2x+35.
【答案】【解答】解:①原式=1+2-(-2)-5,
=0.
②∵x2=2x+35,
∴x2-2x-35=0,
∴(x-7)(x+5)=0,
∴x1=7,x2=-5,
∴原方程的根为:x1=7,x2=-5.
【解析】①根据有理数的乘方,二次根式,立方根,绝对值的性质即可得出答案.
②用十字相乘法因式分解即可求出原方程的根.
【考点精析】关于本题考查的因式分解法和绝对值,需要了解已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,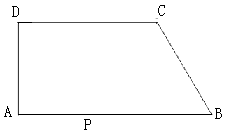
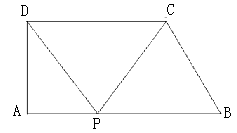
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
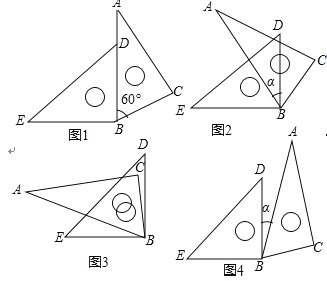
【题目】图1是由一副三角板拼成的图案,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求图1中![]() 的度数;
的度数;
(2)若将图1中的三角板![]() 不动,将另一三角板
不动,将另一三角板![]() 绕点
绕点![]() 顺时针或逆时针旋转
顺时针或逆时针旋转![]() 度(
度(![]() ).当
).当![]() 时,求
时,求![]() 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
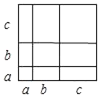
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设⊙B, ⊙M′都与直线l′相切,半径分别为R1、R2 , 当R1+R2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com