
关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
A.m≥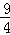 B.m<
B.m<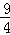 C.m=
C.m=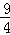 D.m<﹣
D.m<﹣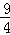
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
某文化商场同时卖出两台电子琴,每台均卖960元.以成本计算,第一台盈利20%,另一台亏本20%.则本次出售中,商场( )
A.不赚不赔 B.赚160元 C.赚80元 D.赔80元
查看答案和解析>>
科目:初中数学 来源: 题型:
一元二次方程x2﹣2(3x﹣2)+(x+1)=0的一般形式是( )
A.x2﹣5x+5=0 B.x2+5x﹣5=0 C.x2+5x+5=0 D.x2+5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
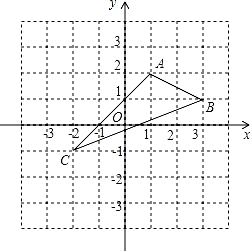
如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.
(2)写出点A1,B1,C1的坐标(直接写答案).
A1
B1
C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
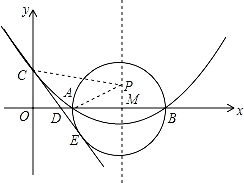
如图,已知抛物线的对称轴为直线l:x=4,且与x轴交于点A(2,0),与y轴交于点C(0,2).
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径作⊙M,过点C作直线CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
请阅读下列材料:
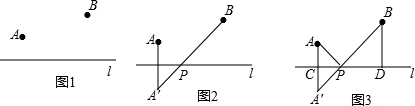
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求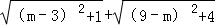 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com