
请阅读下列材料:
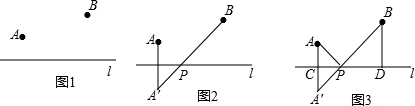
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
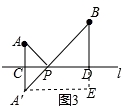
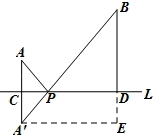
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求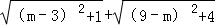 的最小值.
的最小值.
【考点】轴对称-最短路线问题.
【分析】(1)利用勾股定理求得PA,根据三角形相似对应边成比例求得PB,从而求得PA+PB;
(2)作AE∥l,交BD的延长线于E,根据已知条件求得BE、A′E,然后根据勾股定理即可求得A′B,从而求得AP+BP的值;
(3)设AC=1,CP=m﹣3,得到AP=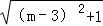 ,设BD=2,DP=9﹣m,得到BP=
,设BD=2,DP=9﹣m,得到BP=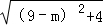 ,于是得到
,于是得到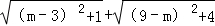 的最小值即为A′B的长,如图,过A′作A′E⊥BD的延长线于点E.根据勾股定理即可得到结论.
的最小值即为A′B的长,如图,过A′作A′E⊥BD的延长线于点E.根据勾股定理即可得到结论.
【解答】解:(1)如图2,∵AA′⊥l,AC=1,PC=1,
∴PA=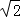 ,
,
∴PA′=PA=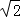 ,
,
∵AA′∥BD,
∴∠A′=∠B,
∵∠A′PC=∠BPD,
∴△A′PC∽△BPD,
∴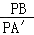 =
=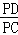 ,
,
∴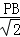 =
=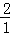 ,
,
∴PB=2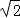 ,
,
∴AP+PB=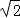 +2
+2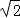 =3
=3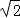 ;
;
故答案为3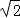 ;
;
(2)作AE∥l,交BD的延长线于E,如图3,
则四边形A′EDC是矩形,
∴AE=DC=PC+PD=3,DE=A′C=AC,
∵BD=4﹣AC,
∴BD+AC=BD+DE=4,
即BE=4,
在RT△A′BE中,A′B=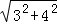 =5,
=5,
∴AP+BP=5,
故答案为5;
(3)设AC=1,CP=m﹣3,
∵A A′⊥L于点C,
∴AP=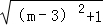 ,
,
设BD=2,DP=9﹣m,
∵BD⊥L于点D,
∴BP=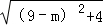 ,
,
∴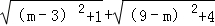 的最小值即为A′B的长.
的最小值即为A′B的长.
即:A′B=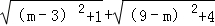 的最小值.
的最小值.
如图,过A′作A′E⊥BD的延长线于点E.
∵A′E=CD=CP+PD=m﹣3+9﹣m=6,BE=BD+DE=2+1=3,
∴A′B=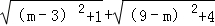 的最小值
的最小值
=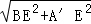
=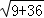
=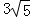 ,
,
∴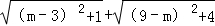 的最小值为
的最小值为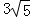 .
.

【点评】本题考查了轴对称﹣最短路线问题,熟练掌握轴对称的性质和勾股定理的应用是解题的关键.


科目:初中数学 来源: 题型:
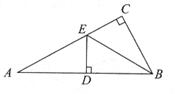
如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com