
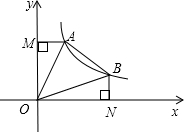
 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y=| k |
| x |
| k |
| x |
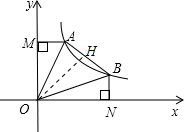 解:设A(x1,y1),B(x2,y2),代入y=
解:设A(x1,y1),B(x2,y2),代入y=| k |
| x |
|
|
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
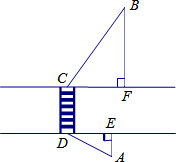 如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)
如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
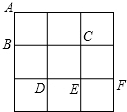 如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、
如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com