【题目】在平面直角坐标系中，己知
为等腰三角形且面积为
,满足条件的
点有( )
A.
个B.
个C.
个D.
个
【答案】D
【解析】
先利用
的面积是9，求得OM边上的高为3，然后分三种情况：①当OM=MN时，②当OM=ON时，③当MN=ON时，分别求得点N的个数，即可得到答案.
∵
，
∴OM=6，
设中，OM边上的高为h，
∴
，解得h=3，
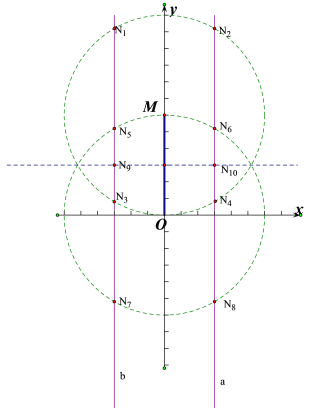
在y轴的两侧作直线a和直线b都和y轴平行，且到y轴的距离都等于3，如图，
①当OM=MN时，
以点M为圆心，以3为半径画圆，交直线a和直线b分别有2个点，即有4个点符合；
②当OM=ON时，
以点O为圆心，以3为半径画圆，交直线a和直线b分别有2个点，即有4个点符合；
③当MN=ON时，
作OM的垂直平分线分别交直线a，b于一点，即有2个点符合；
∴4+4+2=10，
故选D.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，∠ACB=90°，点P是线段AC上一点，过点A作AB的垂线，交BP的延长线于点M，MN⊥AC于点N，PQ⊥AB于点Q，AQ=MN． 求证：
（1）△APM是等腰三角形；
（2）PC=AN．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=
．求证：CB是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在大同市开张的美化城市活动中，某居民小区要在一块一边靠墙（墙长
）的空地上修建一个矩形花园
，花园的一边靠前，另三边用总长为
的栅栏围成（如图所示），若设花园的
长为
，花园的面积为
．
求
与
之间的函数关系式，并写出自变量的取值范围；
满足条件的花园面积能达到
吗？若能，求出此时的值；若不能，说明理由；
根据中求得的函数关系式，描述其图象的变化趋势；并结合题意判断当取何值时，花园的面积最大？最大面积为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两个文具店均出售钢笔和笔记本，其中每支钢笔定价10元，每本笔记本定价5元．两个文具店在开展促销活动中，各自提出优惠方案如下：
甲店：买一支钢笔送一本笔记本；
乙店：买钢笔或笔记本都按定价的80%付款.
现小明要购买钢笔30支，笔记本
本(＞30)．
（1）试用含的代数式表示：
①小明到甲店购买所付款为 元；
②小明到乙店购买所付款为 元；
（2）当
40时，你能帮小明设计一种最为省钱的购买方案吗？试写出你的购买方案，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
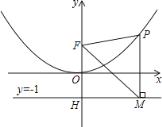
【题目】如图所示，二次函数图象的顶点在原点O，且经过点（1，
）.点F（0，1）在y轴上．直线y=－1与y轴交于点H．
（1）求该二次函数的解析式；
（2）设点P是（1）中图象上在第一象限内的动点，过点P作x轴的垂线与直线y=－1交于点M.
①求证：FM平分∠OFP；
②当△FPM是等边三角形时，试求P点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
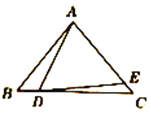
【题目】如图所示，D、E分别是△ABC的边BC、AC上的点，且AB=AC，AD=AE.
（1）若∠BAD=20°，则∠EDC= °.
（2）若∠EDC=20°，则∠BAD= °.
（3）设∠BAD=α，∠EDC=β，你能由（1）（2）中的结果找到α、β间所满足的关系吗?请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，AC=BC=AD．
（1）作∠A的平分线交CD于E；
（2）过B作CD的垂线，垂足为F；
（3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】要建一个如图所示的面积为300
的长方形围栏，围栏总长50m，一边靠墙（墙长25m），
（1）求围栏的长和宽；
（2）能否围成面积为400 的长方形围栏？如果能，求出该长方形的长和宽，如果不能请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com