
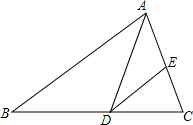
 如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由.
如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
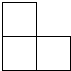 小红分别从正面、左面和上面观察由一些相同小立方块搭成的几何体时,发现几何体的形状图均为如图,则构成该几何体的小立方块的个数有( )
小红分别从正面、左面和上面观察由一些相同小立方块搭成的几何体时,发现几何体的形状图均为如图,则构成该几何体的小立方块的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
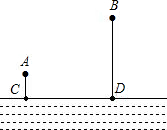 如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
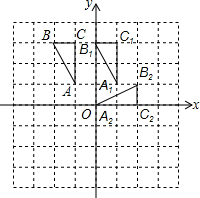 如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题:
如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com