
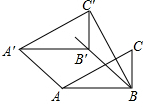
 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )| A. | 6 | B. | 5 | C. | 4$\sqrt{2}$+1 | D. | $\sqrt{41}$ |
分析 如图,延长C′B′交AB于H.首先求出BH,HC′,在Rt△BHC′中,根据BC′=$\sqrt{B{H}^{2}+HC{′}^{2}}$计算即可.
解答 解:如图,延长C′B′交AB于H.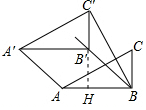
∵∠HBB′=45°,∠BHB′=90°,BB′=4$\sqrt{2}$
∴∠HB′B=∠HBB′=45°,
∴BH=HB′=4,HC′=4+1=5,
在Rt△BHC′中,BC′=$\sqrt{B{H}^{2}+HC{′}^{2}}$=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$,
故选D.
点评 本题考查勾股定理、平移变换、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
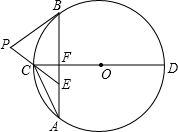 如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
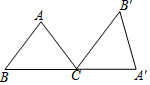 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
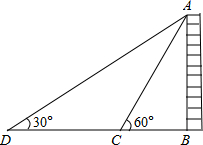 如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).
如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
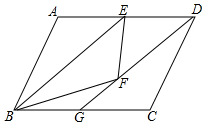 如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.
如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
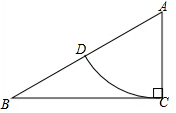 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com