
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
分析 此题要分情况讨论:①两条线段在圆心的同侧,②两条线段在圆心的异侧,然后结合图分别求出两条线段之间的距离即可.
解答 解:①两条线段在圆心的同侧,如图1,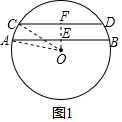
AB=8cm,CD=6cm,且AB∥CD,
先过O作OF⊥CD,垂足是F,交AB于E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=$\frac{1}{2}$AB=4cm,
在Rt△AOE中,AE=4cm,OA=5cm,
∴OE=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
同理可求OF=4cm,
∴EF=OF-OE=1cm;
②两条线段在圆心的异侧,如图2,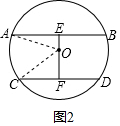
AB=8cm,CD=6cm,且AB∥CD,
先过O作OF⊥CD,垂足是F,反向延长交AB于E,连接OA,OC,
∵AB∥CD,OF⊥CD,
∴OF⊥AB,
∴∠OEA=90°,AE=$\frac{1}{2}$AB=4cm,
在Rt△AOE中,AE=4cm,OA=5cm,
∴OE=$\sqrt{{5}^{2}-{4}^{2}}$=3cm,
同理可求OF=4cm,
∴EF=OE+OF=7cm.
故选C.
点评 本题考查了垂径定理、勾股定理,解题的关键是作辅助线,构造直角三角形,注意分情况讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 “折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.
“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为4.2尺.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).
如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
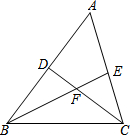 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | 3(x+1)2=2(x+1) | D. | x2-x(x+7)=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
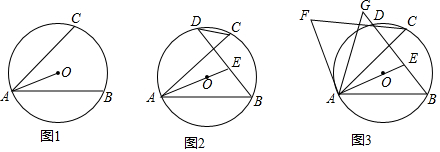
 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
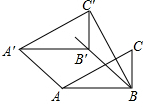 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )| A. | 6 | B. | 5 | C. | 4$\sqrt{2}$+1 | D. | $\sqrt{41}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由x=y,得x+5=y+5 | B. | 由x=y,得$\frac{x}{-2}$=$\frac{y}{-2}$ | ||
| C. | 由-3x=-3y,得x=-y | D. | 由x-1=y-1,得x=y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com