Question

【题目】如图，平面直角坐标系中，四边形OABC是长方形，O为原点，点A在x轴上，点C在y轴上且A(10，0)，C(0，6)，点D在AB边上，将△CBD沿CD翻折，点B恰好落在OA边上的点E处.

(1)求点E、点D的坐标；

(2)求折痕CD所在直线的函数表达式；

(3)请你延长直线CD交x轴于点F，点P是坐标轴上一点请直接写出使S△CEP=S△COF的点P的坐标.

Answer 1

【答案】⑴E（8，0）、D(10，)；⑵CD所在直线的解析式为：y=-x+6；⑶点P的坐标为（2,0）或（14,0）或（0，）或（0，）．

【解析】

（1）由折叠的性质，可得CE=CB=10，在在直角△COE中，由勾股定理求得OE的长，确定E的坐标，设DA=x,则DE=6-x，AE=10-OE=2，运用勾股定理即可确定D的纵坐标，横坐标与点A 相同；

（2）C（0，6），D（10，），利用待定系数法求CD所在直线的解析式；

（3）由（2）得到CD的解析式，令y=0，解得x=18，即F的坐标为（18，0），则△COF的面积为OC×OF；当P在x轴上，设P的坐标为（a，0），则三角形CEP的高为OC,底为8-a，那么面积为OC×（8-a）；当P在y轴上，设P的坐标为（0，b），则三角形CEP的高为OE,底为6-b，那么面积为OE×（6-b）；分别结合三角形COF的面积求解即可.

解：⑴由折叠的性质，可得CE=CB=10，∠CED=90°

又∵OC=6

∴OE=

∴EA=10-8=2

设DA=x,则DE=6-x，

在Rt△EDA中，由勾股定理得：

解得x=

∴E（8，0）、D(10，)；

⑵由题意得：C（0，6），D（10，）

设CD所在的函数解析式为y=kx+b

则有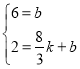 解得

CD所在直线的解析式为：y=-x+6；

⑶如图：

由（2）得CD的解析式y=-x+6；令y=0，解得x=18，即F的坐标为（18,0）

∴OF=18

∴△COF的面积为OC×OF=×6×18=54

∴S△CEP=S△COF=18

①当P在x轴上，设P的坐标为（a，0），则三角形CEP的高为OC,底为|8-a |，那么面积为OC×（8-a）=18，即×6×|8-a |=18，解得a=2或a=14，

∴P的坐标为（2,0）或（14,0）

②设P的坐标为（0，b），则三角形CEP的高为OE,底为6-b，

△CEP面积为OE×|6-b|=18；

即×8×|6-b|=18；

解得b=或b=

点P的坐标为（0，）或（0，）．

综上，P的坐标为（2,0）或（14,0）或（0，）或（0，）．