
【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.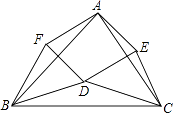
(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
【答案】
(1)△ABF;△BCD
(2)
解:由①知,△ACE∽△BCD,
∴ ![]() ,即
,即 ![]() ,
,
∵∠ECA=∠DCB,
∴∠ECD=∠ACB,
∴△CDE∽△CBA
(3)
证明:∵△CDE∽△CBA,
∴∠ABC=∠EDC,
∵∠ABC=∠FBD,
∴∠EDC=∠FBD,
同理△BFD∽△BAC,
∴∠FDB=∠ACB,
∵∠ACB=∠ECD,
∴∠FDB=∠ACB,
在△FBD与△EDC中 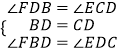 ,
,
∴△FBD≌△EDC;
(4)
解:四边形AFDE是菱形,
理由:∵△FBD≌△EDC,
∴FB=DE,DF=CE,
∵FB=FA,EA=EC,
∴FD=AE,FA=DE,
∴四边形AFDE是平行四边形,
连接AD,则AD平分∠BAC,
即∠BAD=∠CAD,
∵∠BAF=∠CAE,
∴∠DAF=∠DAE,
∵AF∥DE,
∴∠DAF=∠ADE,
∴∠EAD=∠ADE,
∴EA=ED,
∴AFDE是菱形.
【解析】解:(1)∵DB=DC,
∴∠DBC=∠DCB,
∵FB=FA,EA=EC,
∴∠FBA=∠FAB,∠ACE=∠EAC,
∵∠FBA=∠DBC=∠ECA,
∴∠FAB=∠BCD=∠EAC,
∴△ACE∽△ABF∽△BCD;
故答案为:△ABF,△BCD;
(1)根据等腰三角形的性质得到∠DBC=∠DCB,∠FBA=∠FAB,∠ACE=∠EAC,等量代换得到∠FAB=∠BCD=∠EAC,于是得到结论;(2)根据相似三角形的性质得到 ![]() ,根据相似三角形的判定定理即可得到结论;(3)根据相似三角形的性质得到∠EDC=∠FBD,∠FDB=∠ACB等量代换得到∠FDB=∠ACB,根据全等三角形的判定即可得到结论;(4)根据全等三角形的性质得到FB=DE,DF=CE,等量代换得到FD=AE,FA=DE,推出四边形AFDE是平行四边形,连接AD,于是得到AD平分∠BAC,根据菱形的判定定理即可得到结论.
,根据相似三角形的判定定理即可得到结论;(3)根据相似三角形的性质得到∠EDC=∠FBD,∠FDB=∠ACB等量代换得到∠FDB=∠ACB,根据全等三角形的判定即可得到结论;(4)根据全等三角形的性质得到FB=DE,DF=CE,等量代换得到FD=AE,FA=DE,推出四边形AFDE是平行四边形,连接AD,于是得到AD平分∠BAC,根据菱形的判定定理即可得到结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B的大小;
(2)已知b= ![]() ,BD为AC边上的高,求BD的取值范围.
,BD为AC边上的高,求BD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ① ![]() =
= ![]() ;②
;② ![]() =
= ![]() ;③
;③ ![]() ;④
;④ ![]() =
= ![]()
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中线重合,这样得到图②,图③,… 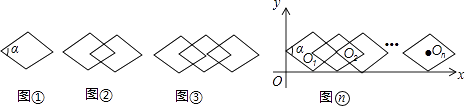
(1)观察以上图形并完成下表:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图(n)中,菱形的个数为(用含有n(n≥3)的代数式表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示. 
(1)求y与x之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加200%,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( ) 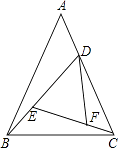
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )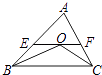
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com