
【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔![]() (
(![]() 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
(2)当购买钢笔多少支时,在两店购买付款一样?
【答案】(1)(5x+300),(4.5x+360);(2)当购买钢笔120支时,在两店购买付款一样.
【解析】
(1)根据实际付款得到甲店购买需付款为5(x﹣20)+20×20,乙店购买需付款为(5x+20×20)×0.9,化简即可得出答案;
(2)令(1)中得出的两个代数式相等,解方程即可得出答案.
解:(1)甲店购买需付款为=5(x﹣20)+20×20=(5x+300)元,
乙店购买需付款为(5x+20×20)×0.9=(4.5x+360)元.
故答案为(5x+300),(4.5x+360);
(2)由(1)知:5x+300=4.5x+360,
解得x=120.
答:当购买钢笔120支时,在两店购买付款一样;


科目:初中数学 来源: 题型:
【题目】某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是( )
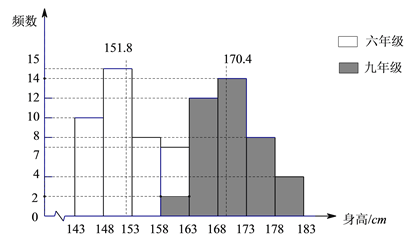
A. 六年级40名男生身高的中位数在第153~158cm组
B. 可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cm
C. 九年级40名男生身高的中位数在第168~173cm组
D. 可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.
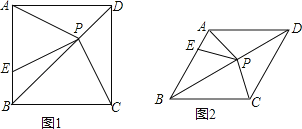
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是________;
(2)请用列表或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜,点P(x,y)在第二象限或第四象限小颖获胜,请分别求出两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧 AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为点D,E;在点C的运动过程中,下列说法正确的是( )
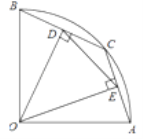
A. 扇形AOB的面积为![]() B. 弧BC的长为
B. 弧BC的长为![]() C. ∠DOE=45° D. 线段DE的长是
C. ∠DOE=45° D. 线段DE的长是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
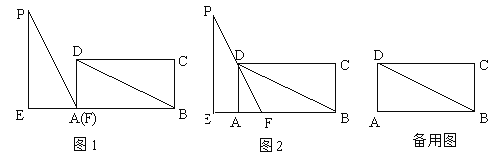
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,点
上的点,点![]() 是一动点.记
是一动点.记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() .
.

(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,如图1,则
,如图1,则![]() _____________;
_____________;
(2)若点![]() 在边
在边![]() 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想![]() ,
,![]() ,
,![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(3)若点![]() 运动到边
运动到边![]() 的延长线上,如图3所示,则
的延长线上,如图3所示,则![]() ,
,![]() ,
,![]() 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
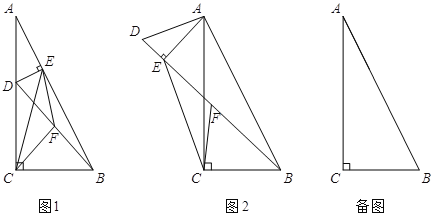
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com