
【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.
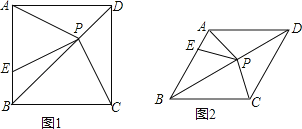
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由.
【答案】(1)见解析;(2)∠EPC=90°;(3)∠ABC+∠EPC=180°.
【解析】
试题分析:(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
 ,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∵PA=PE,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°,
∵∠ABC=90°,
∴∠EPC=90°;
(3)∠ABC+∠EPC=180°,
理由:解:在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP,
∵PA=PE,
∴∠DAP=∠DCP,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
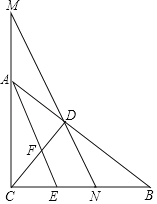
【题目】如图,Rt△ABC中,∠ACB=90°,斜边AB边上的高CD与角平分线AE交于点F,经过垂足D的直线分别交直线CA,BC于点M,N.
(1)若AC=3,BC=4,AB=5,求CD的长;
(2)当∠AMN=32°,∠B=38°时,求∠MDB的度数;
(3)当∠AMN=∠BDN时,写出图中所有与∠CDN相等的角,并选择其中一组进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
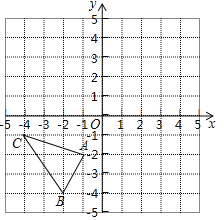
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
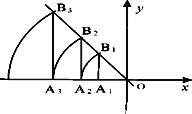
【题目】如图,直线l:y=-![]() x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习:规定:求若干个相同有理数(均不为0)的除法运算叫做除方,如![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() 读作“a的圈n次方”.
读作“a的圈n次方”.
初步探究:
(1)直接写出计算结果![]() ________,
________,![]() ________;
________;
(2)关于除方,下列说法不正确的是________.
A.任何非零数的圈2次方都等于1
B.对于任何正整数n,![]()
![]()
C.![]()
D.负数的圈奇次方结果是负数,负数的圈偶次方结果是正数
深入思考:
我们知道有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:将下列运算结果直接写成幂的形式:![]() ______;
______;![]() ______;
______; ______.
______.
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式为________.
(3)算一算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现了解情况如下:甲、乙两家商店出售两种同样品牌的笔记本和钢笔.笔记本定价为每本20元,钢笔每支定价5元,经洽谈后,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.七年级需笔记本20本,钢笔若干支(不小于20支).问:
(1)如果购买钢笔![]() (
(![]() 不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
不小于20)支,则在甲店购买需付款 ______ 元,在乙店购买需付款 _______________ 元.(用x的代数式表示)
(2)当购买钢笔多少支时,在两店购买付款一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
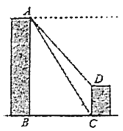
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为58°,求乙建筑物
处的俯角为58°,求乙建筑物![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .结果取整数)
.结果取整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com