
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
【答案】(1) x=﹣1 , AB=4 ;(2) 点P的坐标为(﹣1,﹣ ![]() ).a=
).a= ![]() ; (3) a≥
; (3) a≥ ![]() .
.
【解析】(1)、根据题意求出点A和点B的坐标,从而得出对称轴;(2)、设抛物线的对称轴与x轴交于点H,根据题意得出AH和PH的长度,从而得出点P的坐标,将其代入函数解析式得出a的值;(3)、以AB为直径作⊙H, 当∠ANB=90°, 点N在⊙H上,将x=-1代入y=-4a得出HP的长度,根据题意得出a的取值范围.
(1)、解:令y=0得:ax2+2ax﹣3a=0,即a(x+3)(x﹣1)=0,解得:x=﹣3或x=1,
∴A(﹣3,0)、B(1,0), ∴抛物线的对称轴为直线x=﹣1,AB=4;
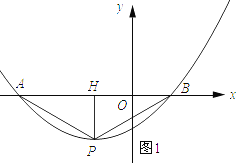
(2)、解:如图1所示:设抛物线的对称轴与x轴交于点H,
∵∠APB=120°,AB=4,PH在对称轴上, ∴AH=2,∠APB=60°, ∴PH= ![]() ,
,
∴点P的坐标为(﹣1,﹣ ![]() ),将点P的坐标代入得:﹣
),将点P的坐标代入得:﹣ ![]() =﹣4a,解得a=
=﹣4a,解得a= ![]() ;
;
(3)、解:如图2所示:以AB为直径作⊙H, ∵当∠ANB=90°, ∴点N在⊙H上,
∵点N在抛物线上, ∴点N为抛物线与⊙H的交点, ∴点P在圆上或点P在圆外,
∴HP≥2, ∵将x=﹣1代入得:y=﹣4a, ∴HP=4a, ∴4a≥2,解得a≥ ![]() ,
,
∴a的取值范围是a≥ ![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最大值为-1,则
的最大值为-1,则![]() 的值为( )
的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式.设一个月内用移动电话主叫为![]()
![]() (
(![]() 是正整数).
是正整数).
月使用费/元 | 主叫限定时间/min | 主 叫 超 时费/(元/min) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |
(1)根据上表,补全下列表.
主叫时间 | 方式一计费/元 | 方式二计费/元 |
| 58 | 88 |
| 58 | 88 |
|
| 88 |
|
| 88 |
|
|
(2)观察(1)中表格,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
(3)小明本月通话时间![]() 分钟.如果采用方式二付费比方式一付费少20.6元;如果通话时间减少70分钟,采用方式二付费比方式一付费少5元.你能确定小明本月通话时长吗?请你通过计算说明.
分钟.如果采用方式二付费比方式一付费少20.6元;如果通话时间减少70分钟,采用方式二付费比方式一付费少5元.你能确定小明本月通话时长吗?请你通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的点,点E在AB上,且PA=PE.
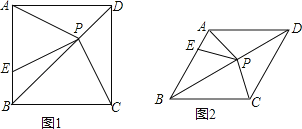
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,试探究∠CPE与∠ABC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧 AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为点D,E;在点C的运动过程中,下列说法正确的是( )
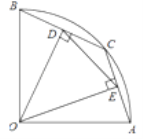
A. 扇形AOB的面积为![]() B. 弧BC的长为
B. 弧BC的长为![]() C. ∠DOE=45° D. 线段DE的长是
C. ∠DOE=45° D. 线段DE的长是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com