
【题目】如图,点![]() 是线段
是线段![]() 上除
上除![]() 外任意一点,分别以
外任意一点,分别以![]() 、
、![]() 为边在线段
为边在线段![]() 的同旁作等边
的同旁作等边![]() 和等边
和等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() .
.

【答案】(1)证明见详解;(2)证明见详解.
【解析】
出现两个等边三角形证全等时,往往要考虑两个三角形的公共角.
证明:∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,
∵∠DCA=∠ECB=60°,
∴∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,
在△ACE与△DCB中,
∵
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)△MNC是等边三角形.理由如下:
∵由(1)得,△ACE≌△DCB,
∴∠CAM=∠CDN,
∵∠ACD=∠ECB=60°,而A、C、B三点共线,
∴∠DCN=60°,
在△ACM与△DCN中,
∵
∴△ACM≌△DCN(ASA),
∴MC=NC,
∵∠MCN=60°,
∴△MCN为等边三角形.
∴∠MCA=∠CMN=60°,
∴MN∥AB.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D在BC边上,点E在AB的延长线上,将DE绕D点顺时针旋转120°得到DF.

(1)如图1,若点F恰好落在AC边上,求证:点D是BC的中点;
(2)如图2,在(1)的条件下,若![]() =45°,连接AD,求证:
=45°,连接AD,求证:![]() ;
;
(3)如图3,若![]() ,连CF,当CF取最小值时,直接写出
,连CF,当CF取最小值时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D,E分别在边AB,AC上,将∠A沿着DE所在直线折叠,A与A′重合,若∠1+∠2=140°,则∠A的度数是( )

A.70°B.75°C.80°D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y1=kx+b经过点P(2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.

(1)求出直线y1=kx+b的解析式;
(2)求出点A的坐标;
(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△PAB是等腰三角形时,点B有几种位置?请你分别求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
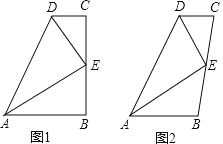
【题目】如图,E 是 BC 的中点,DE 平分∠ADC.
(1)如图 1,若∠B=∠C=90°,求证:AE 平分∠DAB;
(2)如图 2,若 DE⊥AE,求证:AD=AB+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4,

(1)在如图所示的平面直角坐标系中,画出函数的图象.
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标.
(3)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
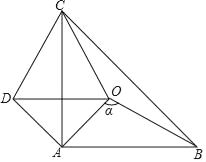
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com