
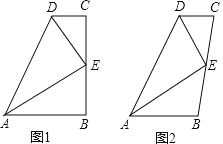
【题目】如图,E 是 BC 的中点,DE 平分∠ADC.
(1)如图 1,若∠B=∠C=90°,求证:AE 平分∠DAB;
(2)如图 2,若 DE⊥AE,求证:AD=AB+CD.
【答案】(1)见解析;(2)见解析.
【解析】
(1)延长 DE 交 AB 的延长线于 F,易得AB∥CD,∠CDE=∠F,又E 是 BC 的中点,可得E 是 BC 的中点,△CDE≌△BFE,可得DE=FE,由已知DE 平分∠ADC,可得∠CDE=∠ADE,∠ADE=∠F,AD=AF,可得结论.
(2)在 DA 上截取 DF=DC,连接 EF, 同理可得△CDE≌△FDE,可得CE=FE,∠CED=∠FED,又E 是 BC 的中点,可得FE=BE,可证得∠AEF=∠AEB,可得
△AEF≌△AEB 可得AF=AB,AD=AF+DF=AB+CD.
解:(1)如图 1,延长 DE 交 AB 的延长线于 F,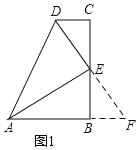
∵∠ABC=∠C=90°,
∴AB∥CD,
∴∠CDE=∠F,
又∵E 是 BC 的中点,
∴E 是 BC 的中点,
∴△CDE≌△BFE(AAS),
∴DE=FE,即 E 为 DF 的中点,
∵DE 平分∠ADC,
∴∠CDE=∠ADE,
∴∠ADE=∠F,
∴AD=AF,
∴AE 平分∠DAB;
(2)如图 2,在 DA 上截取 DF=DC,连接 EF,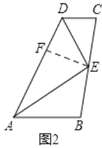
∵DE 平分∠ADC,
∴∠CDE=∠FDE, 又∵DE=DE,
∴△CDE≌△FDE(SAS),
∴CE=FE,∠CED=∠FED, 又∵E 是 BC 的中点,
∴CE=BE,
∴FE=BE,
∵∠AED=90°,
∴∠AEF+∠DEF=90°,∠AEB+∠DEC=90°,
∴∠AEF=∠AEB, 又∵AE=AE,
∴△AEF≌△AEB(SAS),
∴AF=AB,
∴AD=AF+DF=AB+CD.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:
①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是4032亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入增长的平均数比2013年到2015年技术收入增长的平均数大.
其中,正确的是( )
A.①③
B.①④
C.②③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,D ____________ ;
(2)把这些点按A-B-C-D-A顺次连接起来,这个图形的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
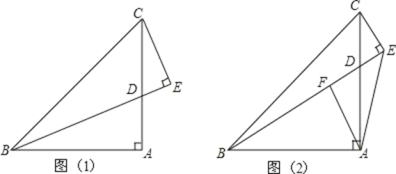
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC请你按要求作图、解答(不写作法,但要保留作图痕迹):
(1)用直尺和圆规,过点B作∠ABC的角平分线交AC于P;
(2)用直尺和直角三角板的直角画PD⊥AB、PE⊥BC垂足分别为D、E;
(3)用刻度尺分别量PD= cm和PE= cm.得PD PE(填大小关系)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用2730元购进A、B两种型号的保温杯共60个,这两种型号的保温杯的进价、标价如表所示:
价格类型 | A型 | B型 |
进价 | 35 | 65 |
标价 | 50 | 100 |
![]() 求这两种型号的保温杯各购进多少个?
求这两种型号的保温杯各购进多少个?
![]() 若A型保温杯按标价的9折出售,要使这批保温杯全部售出后超市获得810元的利润,则B型保温杯应按标价的几折出售?
若A型保温杯按标价的9折出售,要使这批保温杯全部售出后超市获得810元的利润,则B型保温杯应按标价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com