
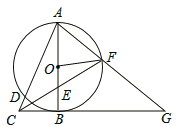
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
【答案】(1)证明过程见解析;(2)DC=![]()
【解析】
试题分析:(1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;(2)首选得出△FOE≌△CBE(ASA),则BC=FO=![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
试题解析:(1)∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在![]() 的中点,∴
的中点,∴![]() =
=![]() ,
,
∴∠AOF=∠BOF, ∵∠ABC=∠ABG=90°, ∴∠AOF=∠ABG, ∴FO∥BG, ∵AO=BO,
∴FO是△ABG的中位线, ∴FO=![]() BG;
BG;
(2)在△FOE和△CBE中,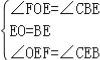 , ∴△FOE≌△CBE(ASA), ∴BC=FO=
, ∴△FOE≌△CBE(ASA), ∴BC=FO=![]() AB=2,
AB=2,
∴AC=![]() =2
=2![]() , 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
, 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
∵∠BCD=∠ACB, ∴△BCD∽△ACB, ∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得:DC=
, 解得:DC=![]() .
.



科目:初中数学 来源: 题型:
【题目】拼图是一种研究代数恒等式的重要方法,所谓的拼图指的是把所给的图形以不同的方式拼成不同形状的图形,把图形面积用不同的代数式表示,由于拼图前后的面积相等,从而相应的代数式的值也相等,进而得到代数恒等式.
(1)智慧学习小组探索了用4个如图1所示的全等的长方形(长、宽分别为a、b)拼成不同的图形.在研究过程中,他们用这4个长方形拼成了一个如图2所示的“回形”正方形.拼图前后,请写出该小组所用图形(4个长方形)的面积的计算方法:拼图前: ;拼图后: ;因为拼图前后的面积不变,所以可得代数恒等式: .

(2)利用(1)中得到的恒等式,解决下面的问题:已知![]() 求xy的值.
求xy的值.
(3)超人学习小组受智慧学习小组的启发,用4个如图3所示的全等的直角三角形(三边长分别为a、b、c)拼成了两种“中空”的正方形.请你画出这两种图形:
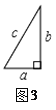
由上面的图形可得代数恒等式: .
(4)利用(3)中得到的代数恒等式,解决下面的问题:在Rt△ABC中,已知∠ABC=90°,AB=6,BC=8,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果![]() ,那么称这个四位数为“和平数”.例如:
,那么称这个四位数为“和平数”.例如:![]() ,因为x=y,所以
,因为x=y,所以![]() 是“和平数”.
是“和平数”.
(1)直接写出:最小的“和平数”是________,最大的“和平数”是________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是![]() 的倍数的所有“和平数”;
的倍数的所有“和平数”;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”。例如:![]() 与
与![]() 为一组“相关和平数”求证:任意的一组“相关和平数”之和是1111的倍数.
为一组“相关和平数”求证:任意的一组“相关和平数”之和是1111的倍数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com