练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：A＝2x2+ax﹣5y+b，B＝﹣bx2+y﹣3．

    （1）求4A﹣（3A+2B）的值；

    （2）当x取任意数值，A﹣2B的值是一个定值时，求的值．

    【答案】（1）4A﹣（3A+2B）＝（2+2b）x2+（a﹣3）x+b+6；（2）1．

    【解析】

    （1）A＝2x2+ax﹣5y+b，B＝﹣bx2+y﹣3 A和B都含有未知数x，y，且都包含二次多项式，和一次多项式x，y，要化简4A﹣（3A+2B），只需将A和B按相同的多项式进行合并即可；

    （2）若要A﹣2B=（2+2b）x2+（a﹣3）x+b+6为定值，也就是说，A和B的多项式x，y前的系数为零。

    （1）∵A＝2x2+ax﹣5y+b，B＝﹣bx2+x﹣y﹣3，

    ∴4A﹣（3A+2B）

    ＝A﹣2B

    ＝2x2+ax﹣5y+b+2bx2﹣3x+5y+6

    ＝（2+2b）x2+（a﹣3）x+b+6；

    （2）由（1）知：A﹣2B＝（2+2b）x2+（a﹣3）x+b+6，

    ∵A﹣2B是一个定值，

    ∴2+2b＝0，且a﹣3＝0，

    ∴a＝3，b＝﹣1，

    ∴（a﹣A）+（b+B）

    ＝（a+b）﹣（A﹣2B）

    ＝1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

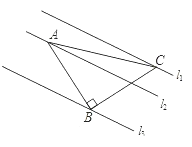
    【题目】如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1、l2之间的距离为2，l2、l3之间的距离为3，则AC的长是_________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：如图1，⊙与直线都相切.不论⊙如何转动，直线之间的距离始终保持不变（等于⊙的半径）.我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面，通过圆棍滚动，用较小的力就可以推动物体前进.据说，古埃及就是利用只有的方法将巨石推到金字塔顶的.

    拓展应用：如图3所示的弧三角形（也称为莱洛三角形）也是“等宽曲线”.如图4，夹在平行线之间的莱洛三角形无论怎么滚动，平行线间的距离始终不变.若直线之间的距离等于，则莱洛三角形的周长为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景:

    小红同学在学习过程中遇到这样一道计算题“计算4×2.112－4×2.11×2.22＋2.222”，她觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!

    获取新知:

    请你和小红一起完成崔老师提供的问题:

    （1）填写下表:

    x＝－1，y＝1

    x＝1，y＝0

    x＝3，y＝2

    x＝2，y＝－1

    x＝2，y＝3

    A＝2x－y

    －3

    2

    4

    5

    1

    B＝4x2－4xy＋y2

    9

    4

    16

    （2）观察表格，你发现A与B有什么关系?

    解决问题:

    （3）请利用A与B之间的关系计算:4×2.112－4×2.11×2.22＋2.222．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=.

    （1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1.

    （2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9,x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）若数轴上两点A、B所表示的数分别为a和b，则有

    ①A、B两点的中点表示的数为；

    ②当b＞a时，A、B两点间的距离为AB＝b﹣a．

    （解决问题）数轴上两点A、B所表示的数分别为a和b，且满足|a+2|+（b﹣8）2020＝0

    （1）求出A、B两点的中点C表示的数；

    （2）点D从原点O点出发向右运动，经过2秒后点D到A点的距离是点D到C点距离的2倍，求点D的运动速度是每秒多少个单位长度？

    （数学思考）（3）点E以每秒1个单位的速度从原点O出发向右运动，同时，点M从点A出发以每秒7个单位的速度向左运动，点N从点B出发，以每秒10个单位的速度向右运动，P、Q分别为ME、ON的中点．思考：在运动过程中，的值是否发生变化？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

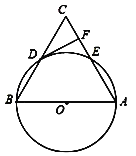
    【题目】如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F.

    (1)求证：DF⊥AC；

    (2)若⊙O的半径为5，∠CDF=30°，求的长(结果保留π)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在《代数式》的学习中,我们通过对同一面积的不同表达和比较,得到合并同类项的法则。下面我们利用这种方法来研究速算。

    （1）提出问题：47×43，56×54，89×81，……是一些十位数相同，且个位数之和是10的两个两位数相乘的算式，是否可以找到一种速算方法？

    （2）几何建模：

    用长方形的面积表示两个正数的乘积，以47×43为例：

    (1)画长为47，宽为43的矩形，如图，将这个47×43的矩形从右边切下长40，宽3的一条，拼接到原长方形上面.

    (2)原长方形面积可以有两种不同的表达方式：47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的长方形面积之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021，

    （3）模仿应用:

    ①请仿照上面的方法使用长方形的面积表示56×54的乘积；

    ②填空：89×81= ×8×100＋ × =7209;

    (4)归纳提炼:

    两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述) .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某出租车司机从公司出发，在东西方向的人民路上连续接送5批客人，行驶路程记录如下(规定向东为正，向西为负，单位：km)：

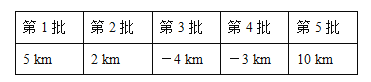
    （1）接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

    （2）若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

    （3）若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

    查看答案和解析>>

    同步练习册答案