
����Ŀ�����Ķ����⣩������������A��B����ʾ�����ֱ�Ϊa��b������
��A��B������е��ʾ����Ϊ![]() ��
��
�ڵ�b��aʱ��A��B�����ľ���ΪAB��b��a��
��������⣩����������A��B����ʾ�����ֱ�Ϊa��b��������|a+2|+��b��8��2020��0
��1�����A��B������е�C��ʾ������
��2����D��ԭ��O����������˶�������2����D��A��ľ����ǵ�D��C������2�������D���˶��ٶ���ÿ����ٸ���λ���ȣ�
����ѧ˼������3����E��ÿ��1����λ���ٶȴ�ԭ��O���������˶���ͬʱ����M�ӵ�A������ÿ��7����λ���ٶ������˶�����N�ӵ�B��������ÿ��10����λ���ٶ������˶���P��Q�ֱ�ΪME��ON���е㣮˼�������˶������У�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
���𰸡���1��A��B������е�C��ʾ������3����2����D���˶��ٶ���ÿ��![]() ����λ���ȣ���ÿ��4����λ���ȣ���3��
����λ���ȣ���ÿ��4����λ���ȣ���3��![]() =2����ֵ�������ɼ�����.
=2����ֵ�������ɼ�����.
��������
��1���ֱ����a��b��ֵ��Ȼ������е�C��ֵ��
��2����������ۣ�����D�˶�����C��ߺ�C�ұ�ʱ���ó���һ����Cֵ��
��3�����˶�ʱ��Ϊt�����E��Ӧ������t����M��Ӧ�����ǩ�2��7t����N��Ӧ������8+10t��![]()
��1����|a+2|+��b��8��2020��0
��a����2��b��8��
��A��B������е�C��ʾ�����ǣ�![]() ��
��
��2�����D���˶��ٶ�Ϊv��
�ٵ���D�˶�����C���ʱ�������⣬��2v������2����2��3��2v����
��֮��![]() ��
��
�ڵ���D�˶�����C�ұ�ʱ�������⣬��2v������2����2��2v��3����
��֮��v��4��
���D���˶��ٶ���ÿ��![]() ����λ���ȣ���ÿ��4����λ���ȣ�
����λ���ȣ���ÿ��4����λ���ȣ�
��3�����˶�ʱ��Ϊt�����E��Ӧ������t����M��Ӧ�����ǩ�2��7t����N��Ӧ������8+10t��
��P��ME���е㣬
��P���Ӧ������![]() ��
��
�֡�Q��ON���е㣬
��Q���Ӧ������![]() ��
��
��MN����8+10t��������2��7t����10+17t��OE��tPQ����4+5t��������1��3t����5+8t��
��![]() ����ֵ��.
����ֵ��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�A(��1��1)��B����4��2����C(��3��4).
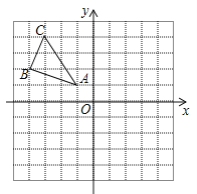
��1���������л�����ABC����ƽ��5����λ���ͼ�Ρ�A1B1C1��
��2���������л�����ABC����ԭ��O�����ĶԳƺ��ͼ�Ρ�A2B2C2��
��3����ֱ��д����B2��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ������֪��A��B��C��D�ֱ�������Բ����������Ľ��㣬�����ߵĽ���ʽΪy��x2��2x��3��ABΪ��Բ��ֱ�������������Բ����y��صõ���CD�ij�Ϊ____��
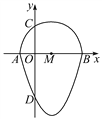
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ����µ�һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ�������һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�β������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ���ͼ1��ABCD�У���AB=1��BC=2����ABCDΪ1�����Σ�
��1����������㣺
�ڱ߳��ֱ�Ϊ3��5��ƽ���ı�����_______�����Σ���֪ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a=8b+r��b=5r����д��ABCD___________��������
��2��������������
С��Ϊ�˼�ȥһ�����Σ����������²�������ͼ2����ABCD��BE�۵�����E��AD�ϣ���ʹ��A����BC���ϵĵ�F�����õ��ı���ABFE����֤���ı���ABFE�����Σ�
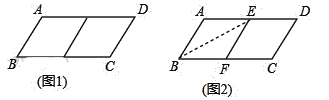
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��2x2+ax��5y+b��B����bx2+![]() y��3��
y��3��
��1����4A����3A+2B����ֵ��
��2����xȡ������ֵ��A��2B��ֵ��һ����ֵʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ��ˮ����©ˮ���������һ̨ˮ�����ˮ��עˮ������8Сʱ���ܽ���ˮ��ע���������ͬ������̨ˮ�����ˮ��עˮ��ֻ��3.2Сʱ���ܽ��ճ�ע������Ҫ��2Сʱ�ھͽ���ˮ��ע����������Ҫ��̨������ˮ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��(+16)��(+5)��(-4);
��2��100��25����-2��
��3��(![]() ��
��![]() ��
��![]() ������
������![]() ��
��
��4��-3����-3������-2����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��F�ֱ���ƽ���ı���ABCD�ı�BC��AD�ϵĵ㣬��BE��DF��
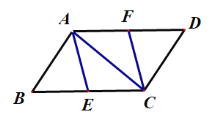
��1����֤���ı���AECFΪƽ���ı��Σ�
��2����AE��BE����BAC��90�㣬�ж��ı���AECF����״��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��������ֽƬ����1�������ĸ���С��״һ����С�����Σ���2�������е�һ��С�������ٰ�ͬ���ķ��������ĸ�С�����Σ�Ȼ���ٽ����е�һ��С�����μ����ĸ�С�����Σ����ѭ��������ȥ���������![]() �Σ�������� ��������.
��������� ��������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com