
【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.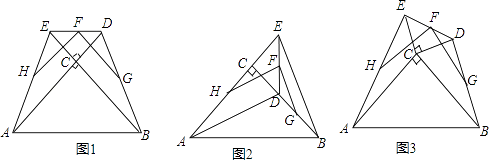
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为和位置关系为;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.
【答案】
(1)相等;垂直
(2)
解:答:成立,
证明:∵CE=CD,∠ECD=∠ACD=90°,AC=BC,
∴△ACD≌△BCE
∴AD=BE,
由(1)知:FH= ![]() AD,FH∥AD,FG=
AD,FH∥AD,FG= ![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,FH⊥FG,
∴(1)中的猜想还成立.
(3)
解:答:成立,结论是FH=FG,FH⊥FG.
连接AD,BE,两线交于Z,AD交BC于X,
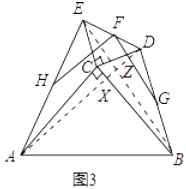
同(1)可证
∴FH= ![]() AD,FH∥AD,FG=
AD,FH∥AD,FG= ![]() BE,FG∥BE,
BE,FG∥BE,
∵三角形ECD、ACB是等腰直角三角形,
∴CE=CD,AC=BC,∠ECD=∠ACB=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中
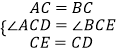 ,
,
∴△ACD≌△BCE,
∴AD=BE,∠EBC=∠DAC,
∵∠DAC+∠CXA=90°,∠CXA=∠DXB,
∴∠DXB+∠EBC=90°,
∴∠EZA=180°﹣90°=90°,
即AD⊥BE,
∵FH∥AD,FG∥BE,
∴FH⊥FG,
即FH=FG,FH⊥FG,
结论是FH=FG,FH⊥FG
【解析】(1)解:∵CE=CD,AC=BC,∠ECA=∠DCB=90°,
∴BE=AD,
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴FH= ![]() AD,FH∥AD,FG=
AD,FH∥AD,FG= ![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,
∵AD⊥BE,
∴FH⊥FG,
所以答案是:相等,垂直.
【考点精析】本题主要考查了等腰直角三角形和三角形中位线定理的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
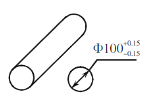
【题目】对某厂生产的一批轴进行检验,检验结果中轴的直径的各组频数、频率如表(每组含前一个边界值,不含后一个边界值),且轴直径的合格标准为![]() (单位:mm),有下列结论:①这批被检验的轴总数为50根;②a+b=0.44且x=y;③这批轴中没有直径恰为100.15mm的轴;④这一批轴的合格率是82%,若该厂生产1000根这样的轴,则其中恰好有180根不合格. 其中正确的有______个.
(单位:mm),有下列结论:①这批被检验的轴总数为50根;②a+b=0.44且x=y;③这批轴中没有直径恰为100.15mm的轴;④这一批轴的合格率是82%,若该厂生产1000根这样的轴,则其中恰好有180根不合格. 其中正确的有______个.
组别(mm) | 频数 | 频率 |
99.55~99.70 | x | a |
99.70~99.85 | 5 | 0.1 |
99.85~100.00 | 21 | 0.42 |
100.00~100.15 | 20 | b |
100.15~100.30 | 0 | 0 |
100.30~100.45 | y | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:
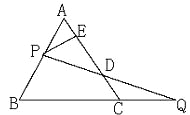
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测) 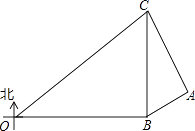
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20 ![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
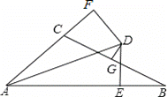
【题目】已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB =12,AC =6,则BE= ___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究题
(1)操作发现:
在△ABC中,AB=AC,∠BAC=90°,D在线段BC上(不与点B重合),连接AD,将线段AD绕A点逆时针旋转90°得到AE,连接EC,如图①所示,请直接写出线段CE和BD的位置关系和数量关系.
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,请你在图②中画出图形并判断(1)中的结论是否成立,并证明你的判断.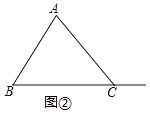
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3 ![]() 时,请直接写出线段CF的长的最大值是 .
时,请直接写出线段CF的长的最大值是 . 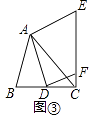
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com