
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测) 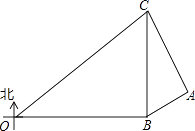
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20 ![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
【答案】
(1)解:在RT△OBC中,∵BO=80,BC=60,∠OBC=90°,
∴OC= ![]() =
= ![]() =100,
=100,
∵ ![]() OC=
OC= ![]() ×100=50
×100=50
∴雷达的有效探测半径r至少为50海里
(2)解:作AM⊥BC于M,
∵∠ACB=30°,∠CBA=60°,
∴∠CAB=90°,
∴AB= ![]() BC=30,
BC=30,
在RT△ABM中,∵∠AMB=90°,AB=30,∠BAM=30°,
∴BM= ![]() AB=15,AM=
AB=15,AM= ![]() BM=15
BM=15 ![]() ,
,
∴此时敌舰A离△OBC海域的最短距离为15 ![]() 海里
海里
(3)解:假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,
∵∠HBN=∠HNB=15°,
∴∠MHN=∠HBN+∠HNB=30°,
∴HN=HB=2x,MH= ![]() x,
x,
∵BM=15,
∴15= ![]() x+2x,
x+2x,
x=30﹣15 ![]() ,
,
∴AN=30 ![]() ﹣30,
﹣30,
BN= ![]() =15(
=15( ![]() ﹣
﹣ ![]() ),设B军舰速度为a海里/小时,
),设B军舰速度为a海里/小时,
由题意 ![]() ≤
≤ ![]() ,
,
∴a≥20.
∴B军舰速度至少为20海里/小时.

【解析】(1)求出OC,由题意r≥ ![]() OC,由此即可解决问题.(2)作AM⊥BC于M,求出AM即可解决问题.(3)假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,先列出方程求出x,再求出BN、AN利用不等式解决问题.
OC,由此即可解决问题.(2)作AM⊥BC于M,求出AM即可解决问题.(3)假设B军舰在点N处拦截到敌舰.在BM上取一点H,使得HB=HN,设MN=x,先列出方程求出x,再求出BN、AN利用不等式解决问题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
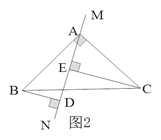
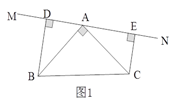
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学老师将本班学生的身高数据(精确到1cm)交给甲、乙两同学,要求他们各自独立地绘制一幅频数直方图,甲绘制的图如图1所示,乙绘制的图如图2所示,经检测确定,甲绘制的频数直方图是正确的,乙在整理数据及绘图过程中均有个别错误.
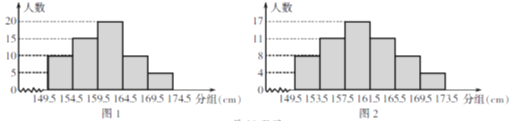
(1)问:该班学生有多少人?
(2)某同学身高为165cm,他说:“我们班上比我高的人不超过![]() .”他的说法正确吗?
.”他的说法正确吗?
(3)请指出乙在整理数据或绘图过程中存在的一个错误.
查看答案和解析>>
科目:初中数学 来源: 题型:
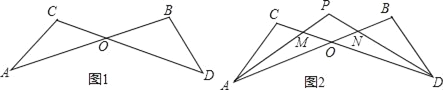
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.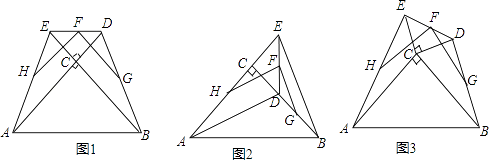
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为和位置关系为;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.
(1)求证:GF=BF;
(2)若△ABC的边长为a,BE的长为b,且a,b满足(a﹣7)2+b2﹣6b+9=0,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
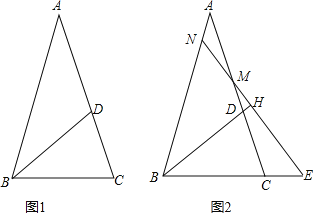
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知抛物线y=ax2+bx﹣3的对称轴为x=1,与x轴分别交于A、B两点,与y轴交于点C,一次函数y=x+1经过A,且与y轴交于点D.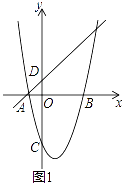
(1)求该抛物线的解析式.
(2)如图(2),点P为抛物线B、C两点间部分上的任意一点(不含B,C两点),设点P的横坐标为t,设四边形DCPB的面积为S,求出S与t的函数关系式,并确定t为何值时,S取最大值?最大值是多少?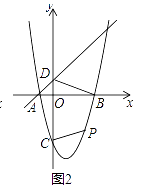
(3)如图(3),将△ODB沿直线y=x+1平移得到△O′D′B′,设O′B′与抛物线交于点E,连接ED′,若ED′恰好将△O′D′B′的面积分为1:2两部分,请直接写出此时平移的距离.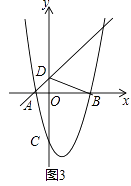
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com