
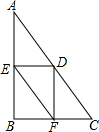 如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.
如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8. 分析 连接BD,根据矩形的性质可知:EF=BD,当BD最小时,则EF最小,根据垂线段最短可知当EF⊥BD时,则EF最小,再根据三角形的面积为定值即可求出EF的长.
解答 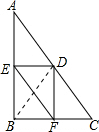 解:∵Rt△ABC中,∠B=90°,AB=8,BC=6,
解:∵Rt△ABC中,∠B=90°,AB=8,BC=6,
∴AC=10,
连接BD,
∵DE⊥AB,DF⊥BC,
∴四边形EBFD是矩形,
∴EF=BD,
当BD最小时,则EF最小,根据垂线段最短可知当BD⊥AC时,则BD最小,
∴EF=BD=$\frac{6×8}{10}$=4.8,
故答案为:4.8.
点评 本题考查了勾股定理的运用、矩形的判定和性质以及直角三角形的面积的不同求法,题目难度不大,设计很新颖,解题的关键是求DE的最小值转化为其相等线段BD的最小值.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
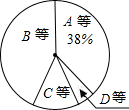 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
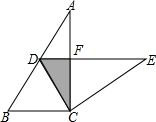 如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转一定角度后得△EDC,点D在AB边上,斜边DE交AC于点F,则图中阴影部分面积为$\frac{\sqrt{3}}{2}$.
如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转一定角度后得△EDC,点D在AB边上,斜边DE交AC于点F,则图中阴影部分面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
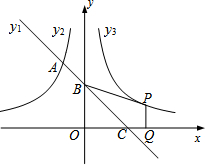 如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.
如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
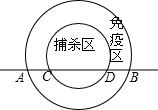 高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com