
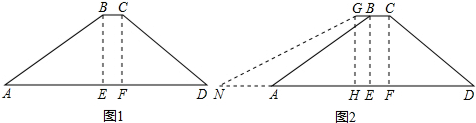
分析 (1)根据坡度和坡高求得AE和DF,然后根据勾股定理即可求得AB,进而即可求得AD;
(2)根据坡度即可求得;
(3)分别求得S梯形GNEB和S△BAE,然后根据S四边形GNAB=S梯形GNEB-S△BAE即可求得.
解答 解:(1)∵斜坡AB的坡度iAB=BE:AE=1:3,BE=23,
∴AE=69,
由勾股定理得,AB=23$\sqrt{10}$,
∵斜坡CD的坡度iCD═CF:DF=1:2.5,CF=23,
∴DF=57.5,
则AD=AE+EF+DF=134.5;
(2)tanα=1:2.5=0.4,
α≈22°;
(3)由题意得,GB=3m,GH=23m,
∵tan∠GNE=$\frac{GH}{NH}$=$\frac{1}{5}$,
∴NH=115m,
∵S梯形GNEB=$\frac{1}{2}$(GB+NE)•BE=$\frac{1}{2}$(3+115+3)×23=$\frac{1}{2}$×121×23,S△BAE=$\frac{1}{2}$BE•AE=$\frac{1}{2}$×23×69
∴S四边形GNAB=S梯形GNEB-S△BAE=$\frac{1}{2}$×121×23-$\frac{1}{2}$×23×69=$\frac{1}{2}$×23×52=498m2.
点评 此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并借助于解直角三角形的知识求解是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
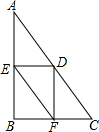 如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.
如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com