
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ�������Σ�

��1������Ϊͼ���е���Ӱ���ֵ������εı߳�����_________________��
��2���������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ������
������ __________________�������� _____________________��
��3���۲�ͼ�ڣ�����д��(m+n)2��(m-n)2��mn����������ʽ֮��ĵ�����ϵ��
��________________________ .
��4�����ݣ�3�����еĵ�����ϵ������������⣺��a+b=6��ab=4������(a-b)2��ֵ��
���𰸡���1��m-n����2����m+n��2-4mn��m-n��2����3����m+n��2-4mn=��m-n��2����4��20��
��������
ƽ���ֳɺ�ÿ��С�����εij�Ϊm����Ϊn��
��1�������εı߳�=С�����εij�-����
��2����һ�ַ���Ϊ�������������-4��С������������ڶ��ֱ�ʾ����Ϊ����Ӱ����ΪС�����ε������
��3�����ã�m+n��2-4mn=��m-n��2����⣻
��4�����ã�a-b��2=��a+b��2-4ab����⣮
��1��m-n��
��2����m+n��2-4mn��m-n��2��
��3����m+n��2-4mn=��m-n��2��
��4����a-b��2=��a+b��2-4ab��
��a+b=6��ab=4��
�ࣨa-b��2=36-16=20��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��4���ӳ�AB����C��ʹ��AB��2BC�������ӳ�AB����D��ʹAC��2AD��
��1�����߶�CD�ij���
��2����QΪAB���е㣬PΪ�߶�CD��һ�㣬��BP��![]() BC�����߶�PQ�ij���
BC�����߶�PQ�ij���
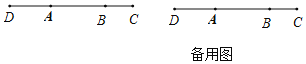
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]()
��1��ֻ����ֱ�ߺ����dzߣ���C����CD��AB����������ͼ�ۼ���
��2��˵��![]() �����ɣ�
�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c�ĶԳ�����x����1���ҹ��㣨![]() ��0���������н��ۣ�
��0���������н��ۣ�
��abc��0����a��2b��4c��0����25a��10b��4c��0����3b��2c��0����a��bm����am��b��������������ȷ�Ľ����У� ������
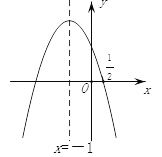
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾��С��ij��������Ӫȫ���ڶ���������������Ͻ��еģ�����涨��Ϊ��������Ϊ����������������ʻ������£�����λ��ǧ����
+15, -3, +14��-11��+10��-12��+4��-15��+16��-18
��1���������һ���˿��͵�Ŀ�ĵ�ʱ������������ص��Ƕ���ǧ�ף�
��2��������������Ϊ![]() ���Mǧ�ף��������繲���Ͷ�����
���Mǧ�ף��������繲���Ͷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016����ʡ�����У���ͼ�٣�����ABC�У���ACB=90�㣬��B=30�㣬AC=1��DΪAB���е㣬EFΪ��ACD����λ�ߣ��ı���EFGHΪ��ACD���ڽӾ��Σ����ε��ĸ����������ACD�ı��ϣ���
��1���������EFGH�������
��2��������EFGH��AB����ƽ�ƣ�F����BC��ʱֹͣ�ƶ�����ƽ�ƹ����У�����������CBD�ص����ֵ����Ϊ![]() ʱ�������ƽ�Ƶľ��룻
ʱ�������ƽ�Ƶľ��룻
��3����ͼ�ۣ�����2���о���ƽ��ֹͣʱ���õľ��μ�Ϊ����E1F1G1H1��������E1F1G1H1��G1�㰴˳ʱ�뷽����ת����H1����CD��ʱֹͣת������ת��ľ��μ�Ϊ����E2F2G1H2������ת��Ϊ������cos����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��鷽ʽ������Ϊ����ʵ��ǣ� ��
A.Ϊ���˽�ͬѧ�Ƕ����ӡ������˴�������Ŀ��ϲ���̶ȣ�С����ѧУ����ɷ���![]() �����꼶ѧ��
�����꼶ѧ��
B.�����������ÿ��Ϸɻ����а��죬���ó������鷽ʽ
C.Ϊ���˽����������꼶ѧ�����������������ȫ����鷽ʽ
D.Ϊ���˽���ʡ�������ƽ���õ��������ó������鷽ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ô����������ϱ�ʾ��һ������Χ�����������Χ���������д���1��С��2������������1��2���������ĵ���ģ���ʾ�����Χ��������1��2����

�����������ϱ�ʾ��һ����Χ��ʹ�������Χ��
��1���������д��ک�3��С��0�������������ᣨ1���ϣ���
��2��������1.5����������������ֻ����5���������������ᣨ2���ϣ���
��3��ͬʱ���������������������������ᣨ3���ϣ�
��������100�Ի�Ϊ�෴����100�Ի�Ϊ������
����������������
�������Χ������������С������ʾ�ĵ�ľ������3��С��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߿Ƽ�������ʶ������ij��ѧ�ڡ�2016��Ƽ��ڡ���о��пƼ���������������ģ�����������ˡ�����������������ģ���ĸ����ÿ��ѧ��ֻ�ܲμ�һ�����ı�������������������ͳ����ͼ��

�����������Ϣ������������⣺
��1��ȫ�������ѧ������ �ˣ�����ģ��������ͳ��ͼ�е�Բ�Ľ��� �㣻
��2��������ͳ��ͼ����������
��3���ڱ�������У���á���������һ�Ƚ���ѧ��Ϊ1��������2��Ů������á���ģ����һ�Ƚ���ѧ��Ϊ1��������1��Ů�����ִ���������һ�Ƚ���ѧ���и����ѡȡ1��ѧ���μ��м���������ģ����������ѡȡ��������ǡΪ1����1Ů���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com