
【题目】如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E. 其中,能使△ABC≌△DEF 的条件共有( )

A. 1 组B. 2 组C. 3 组D. 4 组
科目:初中数学 来源: 题型:
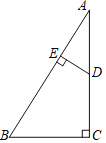
【题目】如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD,BE得到Rt△ABC,已知CD=2,DE=1.
(1)求证:AB=2BC;
(2)求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在整式乘法的学习中,我们采用了构造几何图形的方法研究代数式的变形问题,借助直观、形象的几何图形,加深对整式乘法的认识和理解,感悟代数与几何的内在联系,现有边长分别为![]() ,
,![]() 的正方形Ⅰ号和Ⅱ号,以及长为
的正方形Ⅰ号和Ⅱ号,以及长为![]() ,宽为
,宽为![]() 的长方形Ⅲ号,卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)
的长方形Ⅲ号,卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)
根据已有的学习经验,解决下列问题:

(1)图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形,那么这个几何图形表示的等式是______;

(2)小聪想用几何图形表示等式![]() ,图2给出了他所拼接的几何图形的一部分,请你补全图形;
,图2给出了他所拼接的几何图形的一部分,请你补全图形;

(3)小聪选取2张Ⅰ号卡片、2张Ⅱ号卡片、5张Ⅲ号卡片拼接成一个长方形,请你画出拼接后的长方形,并直接写出几何图形表示的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、C、F、B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为点C、点F,CD=BF.
求证:(1)△ABC≌△EDF;
(2)AB∥DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△![]() 关于直线 PQ 对称,△
关于直线 PQ 对称,△![]() 和△
和△![]() 关于直线 MN对称.
关于直线 MN对称.
(1)用无刻度直尺画出直线MN;
(2)直线 MN 和 PQ 相交于点 O,试探究∠AOA2 与直线 MN,PQ 所夹锐角α的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为 ![]() .
.
(1)则今年南瓜的种植面积为亩;(用含 ![]() 的代数式表示)
的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的 ![]() ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两点(x1 , y1),(x2 , y2) 在函数y= - ![]() 的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
A.y1>y2>0
B.y1<y2<0
C.y2>y1>0
D.y2<y1<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com