
分析 (1)根据约7.2万人,若平均每2人每周从零花钱中节约1元钱(一年按52周计算),求得总共节约的零花钱,再根据小学生平均每年支出约600元(按6年计),初中生平均每年支出约800元(按3年计),进行计算;
(2)设“先进”市小学、中学、高中学生总人数平均每年降低的百分比是x.根据原来是7.2万人,降为5.832万人,列方程求解,再进一步求得帮助的人数.
解答 解:(1)72000÷2×52=1872000(元),
1872000÷(600×6+800×3)=312(人);
(2)设“先进”市小学、中学、高中学生总人数平均每年降低的百分比是x.根据题意,得
7.2(1-x)2=5.832,
解得1-x=±0.9,
x=10%或1.9(不合题意,应舍去).
所以58320÷2×4×52=6065280,(600×6+800×3)×(1-11%)2=4752.6,
6065280÷4752.6≈1276(人).
答:帮助西部山区贫困中小学生读完一至九年级,可以达到1276人.
点评 考查了一元二次方程的应用.此题的文字较多,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.
如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
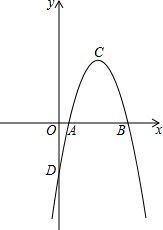 如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=2cm,BC=4cm,动点M从点A出发,以1cm/s的速度沿AB向点B运动;在点M出发的同时,动点N从点B出发,以2cm/s的速度沿BC向点C运动,当点M到达点B时,运动停止.设运动时间为t(s),则当t为何值时,△BMN的面积S(cm2)最大?最大值为多少?
如图,在矩形ABCD中,AB=2cm,BC=4cm,动点M从点A出发,以1cm/s的速度沿AB向点B运动;在点M出发的同时,动点N从点B出发,以2cm/s的速度沿BC向点C运动,当点M到达点B时,运动停止.设运动时间为t(s),则当t为何值时,△BMN的面积S(cm2)最大?最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x+1}{2(x+1)}$ | B. | $\frac{x-y}{{x}^{2}-{y}^{2}}$ | C. | $\frac{3{x}^{2}+x}{{x}^{2}}$ | D. | $\frac{x+1}{{x}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com