
【题目】在平面直角坐标系xOy中,A(4,0),B(0,4),CD是△AOB的中位线.若将△COD绕点O旋转,得到△C′OD′,射线AC′与射线BD′的交点为P.
(1)∠APB的度数是_____°.
(2)在旋转过程中,记P点横坐标为m,则m的取值范围是_____.
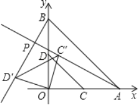
【答案】90°; ![]()
【解析】
(1)由SAS证得△BOD'![]() △AOC',可得∠C'AO=∠D'BO,因为∠BMP=∠AMO,可得∠APB=∠AOB=90°;
△AOC',可得∠C'AO=∠D'BO,因为∠BMP=∠AMO,可得∠APB=∠AOB=90°;
(2)点P在AB为直径的⊙M上运动,过M作PM∥OA交⊙M于点P(在点M的左侧),此时m的值最小;当BD′与⊙O相切时,m最大,分别求出对应m的值,即可得出m的取值范围.
(1)如图1,
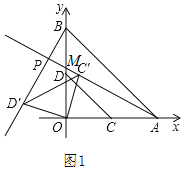
∵A(4,0),B(0,4),
∴OA=OB,∠AOB=90°,
∵CD是△AOB的中位线,
∴CO=DO=2=BD=AC,
∵将△COD绕点O旋转,得到△C′OD′,
∴CO=DO,∠C'OD'=90°=∠AOB,
∴∠BOD'=∠AOC',且C'O=D'O,AO=BO,
∴△BOD![]() △AOC'(SAS)
△AOC'(SAS)
∴∠C'AO=∠D'BO,
∵∠BMP=∠AMO,
∴∠APB=∠AOB=90°,
故答案为:90,
(2)如图2,
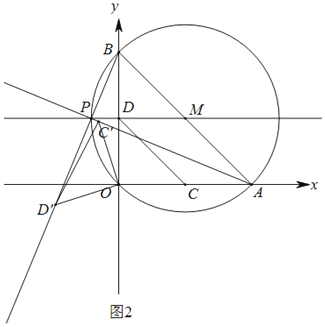
∵∠BPA=90°,
∴点P在AB为直径的⊙M上运动,
过M作PM∥OA交⊙M于点P(在点M的左侧),此时m的值最小,
∵AB=4![]() ,DM=2,
,DM=2,
∴PD=2![]() 2,
2,
∴m=22![]() .
.
如图3,
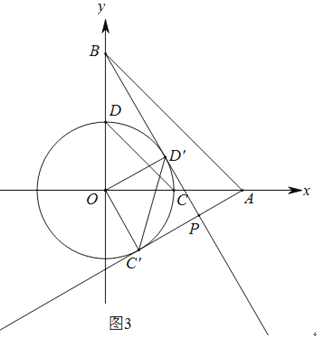
∵OD′=OC′=2,
∴点D′,点C′在⊙O上运动,
当BD′与⊙O相切时,m最大,
此时BD′=![]() ,D′P=OC′=2,
,D′P=OC′=2,
∴BP=2![]() +2,
+2,
∵OB4,OD′=2,
∴sin∠OBD′=![]() ,
,
∴m=![]() BP=
BP=![]() +1,
+1,
∴22![]() ≤m≤
≤m≤


科目:初中数学 来源: 题型:
【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=![]() ;
;
④∠ACB=50°.其中错误的是( )
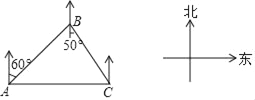
A. ①② B. ②④ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

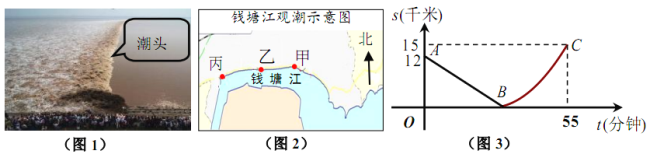
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数
可用二次函数![]() (
(![]() ,
,![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=mx2+(5m+3)x+4m(m为常数且m≠0)有以下三种说法:
①不论m为何值,函数图象一定过定点(﹣1,﹣3);
②当m=﹣1时,函数图象与坐标轴有3个交点;
③当m<0,x≥﹣![]() 时,函数y随x的增大而减小;判断真假,并说明理由.
时,函数y随x的增大而减小;判断真假,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD,边长等于2,点E、F、G、H分别是AB、BC、CD、DA的中点,图中阴影部分由四个小扇形组成,对于下列判断中正确的有( )
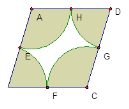
①空白图形空白部分的周长=2![]() ②空白部分的面积=
②空白部分的面积=![]()
③四个小扇形的面积和 =![]() ④菱形的面积=4
④菱形的面积=4
A 1个 B 2个 C 3个 D 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
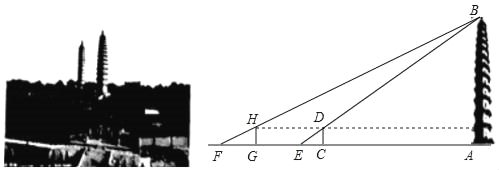
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
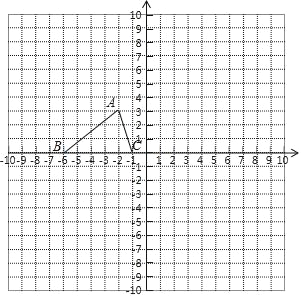
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点P的坐标 .
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点Q的坐标 .
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com