
【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
【答案】(1)y=﹣10x2+90x+1900;(2)每件商品的售价定为61元或68元时,每天的利润恰为1980元;(3)每件商品的售价定为64.5元时,每天可获得最大利润,最大利润是2102.5元.
【解析】试题分析:(1)利用销量乘以每件利润=总利润得出关系式即可;
(2)利用(1)中所求关系式,进而使y=1980进而得出即可;
(3)利用配方法求出二次函数最值,结合x的取值范围得出答案.
试题解析:(1)设每件商品的售价上涨x元,每天的销售利润为y元,
则y=(60﹣50+x)(190﹣10x)=﹣10x2+90x+1900;
(2)当y=1980,则1980=﹣10x2+90x+1900,
解得:x1=1,x2=8.
故每件商品的售价定为61元或68元时,每天的利润恰为1980元;
(3)y=﹣10x2+90x+1900=﹣10(x﹣![]() )2+2102.5,
)2+2102.5,
故当x=4.5时,y=2102.5(元),
即每件商品的售价定为64.5元时,每天可获得最大利润,最大利润是2102.5元.


科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
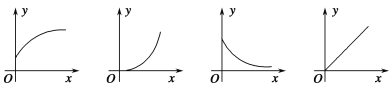
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“![]() ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如: ![]() ,
,
∵![]() ≥0,
≥0,
∴![]() ≥1,
≥1,
∴![]() ≥1.
≥1.
试利用“配方法”解决下列问题:
(1)填空: ![]() (x )2+ ;
(x )2+ ;
(2) 已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
(3)比较代数式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
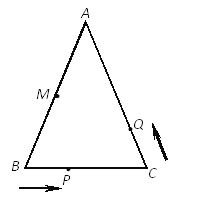
【题目】如图,已知△ABC中,AB=AC=12厘米,(即∠B=∠C),BC=9厘米,点M为AB的中点,
(1)如果点P在线段BC上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1.5秒后,△BPM与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPM与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
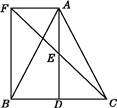
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
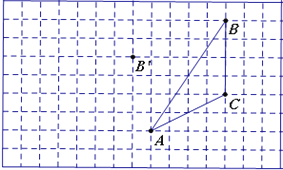
(1) 补全△A′B′C′;
(2) 根据下列条件,利用网格点和直尺画图:
画出△ABC中:
①AC边上的中线BD;
②AC边上的高线BE;
(3)写出△ABD的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
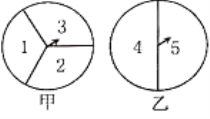
【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com