【题目】如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
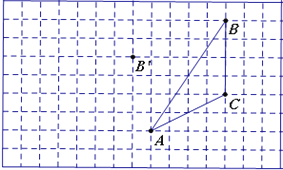
(1) 补全△A′B′C′；
(2) 根据下列条件，利用网格点和直尺画图：
画出△ABC中：
①AC边上的中线BD；
②AC边上的高线BE；
(3)写出△ABD的面积 ．
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝2x2－mx－m2.
(1)求证：对于任意实数m，二次函数y＝2x2－mx－m2的图象与x轴总有公共点；
(2)若这个二次函数的图象与x轴有两个公共点A，B，且B点坐标为(1，0)，求A点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商品的进价为每件50元，售价为每件60元，每天可卖出190件；如果每件商品的售价每上涨1元，则每天少卖10件，设每件商品的售价上涨x元，每天的销售利润为y元．
（1）求y关于x的关系式；
（2）每件商品的售价定为多少元时，每天的利润恰为1980元？
（3）每件商品的售价定为多少元时，每天可获得最大利润？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家－“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.
以
为例，花拉子米的几何解法如下：
如图，在边长为
的正方形的两个相邻边上作边长分别为
和5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形.
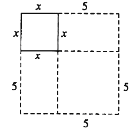
通过不同的方式来表达大正方形的面积，可以将原方程化为
）2=39+ ，从而得到此方程的正根是 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 |
B．平方差公式 |
C．两数和的完全平方公式 |
D．两数差的完全平方公式 |
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题：①相等的角是对顶角；②在同一平面内，若a∥b，b∥c，则a∥c；③同旁内角互补；④互为邻补角的两角的角平分线互相垂直．⑤平面内，过一点能且只能作一条直线与已知直线垂直．其中真命题有______（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面4个说法中，正确的个数为( )．
(1)“从袋中取出一只红球的概率是99％”，这句话的意思是肯定会取出一只红球，因为概率已经很大
(2)袋中有红、黄、白三种颜色的小球，这些小球除颜色外没有其他差别，因为小张对取出一只红球没有把握，所以小张说：“从袋中取出一只红球的概率是50％”
(3)小李说，这次考试我得90分以上的概率是200％
(4)“从盒中取出一只红球的概率是0”，这句话是说取出一只红球的可能性很小
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，三角形ABC（记作△ABC）在方格中，方格纸中的每个小方格都是边长为1个单位的正方形，三个顶点的坐标分别是A（﹣2，1），B（﹣3，﹣2），C（1，﹣2），先将△ABC向上平移3个单位长度，再向右平移2个单位长度，得到A1B1C1．
（1）在图中画出△A1B1C1；
（2）点A1，B1，C1的坐标分别为 、 、 ；
（3）若y轴有一点P，使△PBC与△ABC面积相等，求出P点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
