
| 点的个数 | 2 | 3 | 4 | 5 | … | 2016 | … | n |
| 能做直线最多条数 | 1 | 3 | 6 | / | … | 2031120 | … | $\frac{n(n-1)}{2}$ |
分析 (1)分五种情况考虑,画出草图,数出直线的条数即可得出结论;
(2)设平面内有n(n为不小于2的整数)个点,过这n个点最多能作an条直线,根据部分an的变化找出变化规律“an=$\frac{n(n-1)}{2}$”,依此即可得出结论.
解答 解:(1)①若5个点在一条直线上,只能确定1条直线;
②若只有4个点在一条直线上,则能确定5条直线;
③若有两个3个点在一条直线上,则能确定6条直线;
④若只有3点在一条直线上,则能确定8条直线;
⑤若没有任何3点在一条直线上,则能确定10条直线.
(2)设平面内有n(n为不小于2的整数)个点,过这n个点最多能作an条直线,
观察,发现规律:a2=$\frac{2×1}{2}$=1,a3=$\frac{3×2}{2}$=3,a4=$\frac{4×3}{2}$=6,a5=$\frac{5×4}{2}$=10,…,
∴an=$\frac{n(n-1)}{2}$.
当n=2016时,a2016=$\frac{2016×2015}{2}$=2031120.
故答案为:2031120;$\frac{n(n-1)}{2}$.
点评 本题考查了直线、射线、线段以及规律型中数字的变化,解题的关键是:(1)分五种情况考虑;(2)找出变化规律“an=$\frac{n(n-1)}{2}$”.


科目:初中数学 来源: 题型:解答题
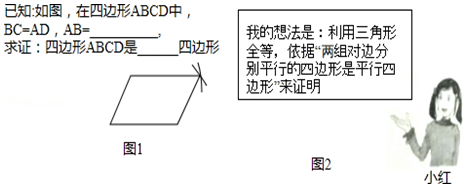
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
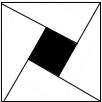 如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.
如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com