
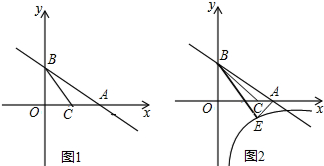
分析 (1)先求出A点和B点坐标,设C(t,0),则AC=4-t=BC,在Rt△OBC中利用勾股定理得22+t2=(4-t)2,然后解方程求出t的值即可得到点C的坐标;
(2)延长AE交y轴于F,BE交x轴于点D,如图,先证明Rt△ABO∽Rt△FAO,利用相似比求出OF=8,则F(0,-8),于是可根据待定系数法求出直线AF的解析式为y=2x-8,
由于BD平分∠OBC,根据角平分线定理得到$\frac{OD}{CD}$=$\frac{OB}{BC}$=$\frac{4}{5}$,而OD+CD=$\frac{3}{2}$,则可计算出OD=$\frac{2}{3}$,得到D($\frac{2}{3}$,0),然后利用待定系数法求出直线BD的解析式为y=-3x+2,接着根据两直线的交点问题通过解方程组$\left\{\begin{array}{l}{y=-3x+2}\\{y=2x-8}\end{array}\right.$得E点坐标为(2,-4),最后根据反比例函数图象上点的坐标特征求k的值.
解答 解:(1)当x=0时,y=-$\frac{1}{2}$x+2=2,则B(0,2),
当y=0时,=-$\frac{1}{2}$x+2=0,解得x=4,则A(4,0),
设C(t,0),则AC=4-t,
∵AC=BC,
∴BC=4-t,
在Rt△OBC中,∵OB2+OC2=BC2,
∴22+t2=(4-t)2,解得t=$\frac{3}{2}$,
∴点C的坐标为($\frac{3}{2}$,0);
(2)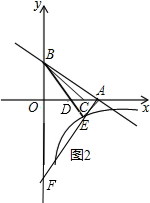 延长AE交y轴于F,BE交x轴于点D,如图,
延长AE交y轴于F,BE交x轴于点D,如图,
∵AE⊥AB,
∴∠BAO+∠FAO=90°,
∵∠BAO+∠OBA=90°,
∴∠OBA=∠FAO,
∴Rt△ABO∽Rt△FAO,
∴$\frac{OB}{OA}$=$\frac{OA}{OF}$,即$\frac{2}{4}$=$\frac{4}{OF}$,解得OF=8,
∴F(0,-8),
设直线AF的解析式为y=ax+b,
把A(4,0),F(0,-8)分别代入得$\left\{\begin{array}{l}{4a+b=0}\\{b=-8}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-8}\end{array}\right.$,
∴直线AF的解析式为y=2x-8,
∵B(0,2),C($\frac{3}{2}$,0),
∴BC=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,
∵BD平分∠OBC,
∴$\frac{OD}{CD}$=$\frac{OB}{BC}$=$\frac{2}{\frac{5}{2}}$=$\frac{4}{5}$,
而OD+CD=$\frac{3}{2}$,
∴OD+$\frac{5}{4}$OD=$\frac{3}{2}$,解得OD=$\frac{2}{3}$,
∴D($\frac{2}{3}$,0),
设直线BD的解析式为y=mx+n,
把B(0,2),D($\frac{2}{3}$,0)分别代入得$\left\{\begin{array}{l}{n=2}\\{\frac{2}{3}m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-3}\\{n=2}\end{array}\right.$,
∴直线BD的解析式为y=-3x+2,
解方程组$\left\{\begin{array}{l}{y=-3x+2}\\{y=2x-8}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$,
∴E点坐标为(2,-4),
∴E点在双曲线$y=\frac{k}{x}$(x>0)上,
∴k=2×(-4)=-8.
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和一次函数图象上点的坐标特征;会利用待定系数法求一次函数解析式;会求两一次函数图象的交点坐标.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
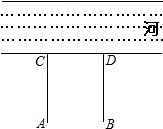 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$-$\sqrt{6}$ | B. | 6-$\sqrt{2}$ | C. | 6-$\sqrt{6}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
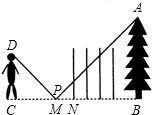 王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.
王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com