
����Ŀ����ͼ��Rt![]() ABC�У���C��90����AC��10��BC��16������P��ÿ��3����λ���ٶȴӵ�A��ʼ���C�ƶ���ֱ��l����AC�غϵ�λ�ÿ�ʼ������ͬ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P�ƶ������C�غ�ʱ����P��ֱ��lͬʱֹͣ�˶������ƶ������У���
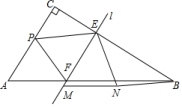
ABC�У���C��90����AC��10��BC��16������P��ÿ��3����λ���ٶȴӵ�A��ʼ���C�ƶ���ֱ��l����AC�غϵ�λ�ÿ�ʼ������ͬ���ٶ���CB����ƽ���ƶ����ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P�ƶ������C�غ�ʱ����P��ֱ��lͬʱֹͣ�˶������ƶ������У���![]() PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����ֱ��l�ϣ���F�Ķ�Ӧ���Ϊ��N������BN����BN��PEʱ��t��ֵΪ_____��
PEF�Ƶ�E��ʱ����ת��ʹ�õ�P�Ķ�Ӧ��M����ֱ��l�ϣ���F�Ķ�Ӧ���Ϊ��N������BN����BN��PEʱ��t��ֵΪ_____��
���𰸡�![]()
��������
��NH��BC��H������֤����PEC����NEB����NBE���Ƴ�EH��BH������cos��PEC��cos��NEB���Ƴ�![]() ��
��![]() ���ɴ˹������̽�����⼴�ɣ�
���ɴ˹������̽�����⼴�ɣ�
�⣺��NH��BC��H��
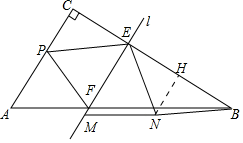
��EF��BC����PEF����NEF��
���FEC����FEB��90����
�ߡ�PEC+��PEF��90������NEB+��FEN��90����
���PEC����NEB��
��PE��BN��
���PEC����NBE��
���NEB����NBE��
��NE��NB��
��HN��BE��
��EH��BH��
��cos��PEC��cos��NEB��
��![]() ��
��![]() ��
��
��EF��AC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��EF��EN��![]() (16��3t)��
(16��3t)��
��![]() ��
�� ��
��
�����ã�63t2��960t+1600��0��
���t��![]() ��
��![]() (����)��
(����)��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��֯����֪ʶ������ÿ��μӾ�����������ͬ���ɼ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֣�90�֣�80�֣�70�֣�����100�ֺ�90��Ϊ����.ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��ͳ�Ʊ�.
�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֣�90�֣�80�֣�70�֣�����100�ֺ�90��Ϊ����.ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��ͳ�Ʊ�.
һ�ྺ���ɼ�ͳ��ͼ
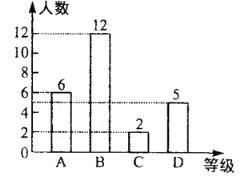
���ྺ���ɼ�ͳ��ͼ
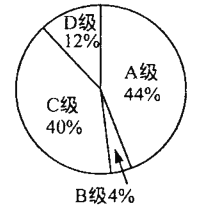
һ��Ͷ��ྺ���ɼ�ͳ�Ʊ������ֿ�ȱ��
�ɼ� �༶ | ���� | ��λ�� | ������ | ƽ���� |
һ�� | 90 |
|
| 87.6 |
���� |
| 80 |
|
|
���������ͼ������Ϣ����������⣺
��1����![]() ��
��![]() ��
��![]() ��ֵ.
��ֵ.
��2����ȫУ����750��ѧ���μӾ��������Ƴɼ������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ����������ABCD�Ķ���A�ڣ����ϣ�����D�ڷ���������y����x>0����ͼ���ϣ���֪��B����������![]() ��
��![]() ������k��ֵΪ�� ��
������k��ֵΪ�� ��
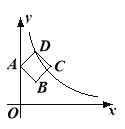
A��10 B��8 C��6 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����A��m��6����B��3��n������.
��ͼ����A��m��6����B��3��n������.
��1����һ�κ����Ľ���ʽ��
��2����![]() �������
�������
��3������ͼ��ֱ��д��![]() ��x��ȡֵ��Χ
��x��ȡֵ��Χ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
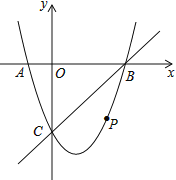
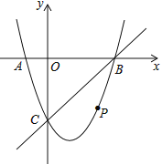
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣬
���㣬![]() ����ԭ�����࣬
����ԭ�����࣬![]() �������Ϊ��
���������![]() ��
��![]() ������
������![]() �ύ��
�ύ��![]() ��
��![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() �·�����������һ����.
�·�����������һ����.
��1����������κ����ı���ʽ��
��2������![]() ��
��![]() �����ѡ�
�����ѡ�![]() ��
��![]() �߷��ۣ��õ��ı���
�߷��ۣ��õ��ı���![]() �� ��ô�Ƿ���ڵ�
�� ��ô�Ƿ���ڵ�![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊ���Σ������ڣ��������ʱ��
Ϊ���Σ������ڣ��������ʱ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
��3������![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �������������ʱ
�������������ʱ![]() ���������ı���
���������ı���![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�����������������Դ�����ã���ϵ�������Ⱥ�����������ϵ��Լʹ����Դ��Ҳ���������ˮƽ��һ����Ҫ����.ij������˾�з��˼ס������������豸�����������¼��������������з�ѡ�����Ƴɹ̻�����ȼ�ϰ����������ɴ˱����������ȼ��.ij�����������ӻ�����˾�����������������豸���ɣ���֪������������豸����![]() ��Ԫ���������������豸����
��Ԫ���������������豸����![]() ��Ԫ������������豸������ͬ�������������豸�ĵ��ۺ�Ϊ
��Ԫ������������豸������ͬ�������������豸�ĵ��ۺ�Ϊ![]() ��Ԫ.
��Ԫ.
![]() ��ס������������豸���ۣ�
��ס������������豸���ۣ�
![]() �������������������豸����ȼ�ϰ���������Ʒ����.��֪ȼ�ϰ��ijɱ��������ɱ������ʳɱ���������ɣ��������ʳɱ�ռ�ܳɱ���
�������������������豸����ȼ�ϰ���������Ʒ����.��֪ȼ�ϰ��ijɱ��������ɱ������ʳɱ���������ɣ��������ʳɱ�ռ�ܳɱ���![]() ��������ÿ��ȼ�ϰ����������ɱ������ʳɱ��ı�
��������ÿ��ȼ�ϰ����������ɱ������ʳɱ��ı�![]() ����
����![]() Ԫ.���鷢�֣���ȼ�ϰ��ۼ�Ϊÿ��
Ԫ.���鷢�֣���ȼ�ϰ��ۼ�Ϊÿ��![]() Ԫ��ƽ��ÿ����۳�
Ԫ��ƽ��ÿ����۳�![]() �֣��������ۼ�ÿ����
�֣��������ۼ�ÿ����![]() Ԫ��ƽ��ÿ��ɶ��۳�
Ԫ��ƽ��ÿ��ɶ��۳�![]() ��.������������ʹ����ȼ�ϰ�����������ƽ��ÿ��ﵽ
��.������������ʹ����ȼ�ϰ�����������ƽ��ÿ��ﵽ![]() Ԫ���ұ�֤�ۼ���ÿ��
Ԫ���ұ�֤�ۼ���ÿ��![]() Ԫ�����Ͻ��۷��Ȳ�����
Ԫ�����Ͻ��۷��Ȳ�����![]() ����ÿ��ȼ�ϰ��ۼ�ӦΪ����Ԫ��
����ÿ��ȼ�ϰ��ۼ�ӦΪ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ÿ�������2022�걱�����»����Ҫ��ͨ������ʩ�����ǵ���ͬ·�ε���������������ݲ�ͬ�������������ò�ͬ��ʱ�٣����б�����վ�����վ��Ϊ���µ��廪����12ǧ�͵��ϵ���Ӷ�10ǧ�������֣���������ϵ������ٶ�֮��Ϊ![]() �����±ȵ��ϵ�����ʱ���2���ӣ���ͨ�����µ��廪����������ٶȣ�
�����±ȵ��ϵ�����ʱ���2���ӣ���ͨ�����µ��廪����������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=![]() ��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��1�����������Ľ���ʽ��B������ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��BD���ӳ����ϣ��ҡ�EAC�ǵȱ������Σ�
��1����֤���ı���ABCD�����Σ�
��2����AC=8��AB=5����ED�ij���
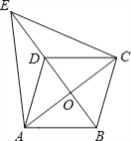
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com