
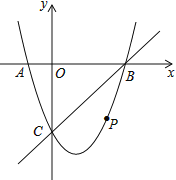
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),与
),与![]() 轴交于
轴交于![]() (
(![]() ,
,![]() ),点
),点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结![]() 、
、![]() ,并把△
,并把△![]() 沿
沿![]() 边翻折,得到四边形
边翻折,得到四边形![]() , 那么是否存在点
, 那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大并求出此时
的面积最大并求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)y=x2-2x-3;(2)存在, ;(3)当点P的坐标为
;(3)当点P的坐标为![]() ,四边形
,四边形![]() 的面积最大,最大面积是
的面积最大,最大面积是![]()
【解析】
(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;.
(2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标;.
(3)由于△ABC的面积为定值,当四边形ABPC的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线BC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC的面积,由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标.
(1)将B、C两点的坐标代入![]() ,
,
得![]() ,解得
,解得![]() ,
,
∴二次函数的解析式为y=x22x3;
(2)存在点P,使四边形POP′C为菱形,
设P点坐标为(x,x2-2x-3),PP′交CO于E,
若四边形POP′C是菱形,则有PC=PO,
连接PP′,则PE⊥CO于E,
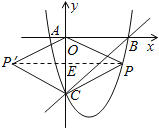 .
.
∵C(0,-3),
∴CO=3,
又∵OE=EC,
∴OE=EC=![]() ,
,
∴y=![]() ;
;
∴x2-2x-3=![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴存在这样的点,此时P点的坐标为 ;
;
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3),
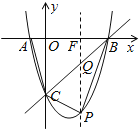
设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]()
∴直线BC的解析式为y=x-3,
则Q点的坐标为(x,x-3),
当0=x2-2x-3,
解得:x1=-1,x2=3,
∴AO=1,AB=4,
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF
QPOF
=![]() ×4×3+
×4×3+![]() (x2+3x)×3
(x2+3x)×3
=![]() (x
(x![]() )2+
)2+![]()
当x=![]() 时,四边形ABPC的面积最大,
时,四边形ABPC的面积最大,
此时P点的坐标为(![]() ,
,![]() ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
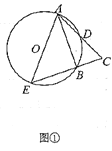
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
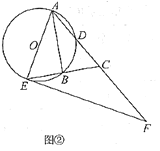
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
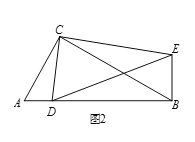
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
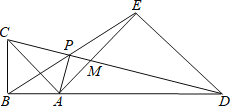
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
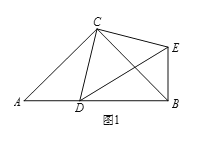
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
(3)拓展延伸
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
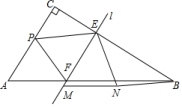
【题目】如图,Rt![]() ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将
ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将![]() PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一枚木质中国象棋子“兵”从一定高度落下,落地后“兵”字面可能朝上,也可能朝下.为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验数据如下表:
实验次数 | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数 | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 | 0.7 | 0.63 | 0.52 | 0.55 | 0.56 | 0.55 | 0.56 | 0.55 | 0.55 | 0.55 |
下面有三个推断:①投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是0.55;②随着实验次数的增加,“兵”字面朝上的频率总在0.55附近,显示出一定的稳定性,可以估计“兵”字面上的概率是0.55;③当实验次数为200次时,“兵”字面朝上的频率一定是0.55.其中合理的是______.(填序号①、②、③)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】速滑运动受到许多年轻人的喜爱,如图,梯形BCDG是某速滑场馆建造的速滑台,已知CD∥EG,高DG为4米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为1:![]() .
.
(1)求新坡面AC的坡角;
(2)原坡面底部BG的正前方10米(EB的长)处是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由.(参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为![]() .
.
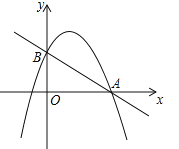
(1)求二次函数![]() 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足![]() 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com