
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
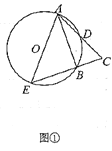
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
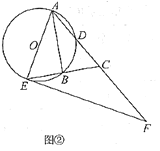
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
科目:初中数学 来源: 题型:
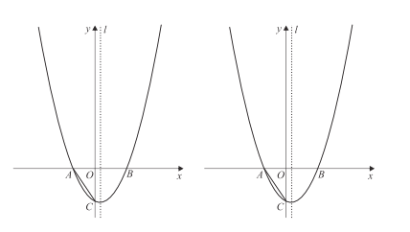
【题目】如图,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线的函数表达式和直线![]() 的解析式;
的解析式;
(2)若点![]() 在第二象限内,且
在第二象限内,且![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,若![]() 为直线
为直线![]() 上一点,是否存在点
上一点,是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
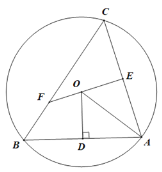
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于![]() 及一个矩形给出如下定义:如果
及一个矩形给出如下定义:如果![]() 上存在到此矩形四份顶点距离都相等的点,那么称
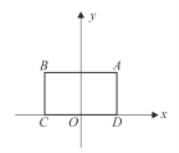
上存在到此矩形四份顶点距离都相等的点,那么称![]() 是该矩形的“等距圆”,如图,平面直角坐标系
是该矩形的“等距圆”,如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() 的半径为
的半径为![]() .
.
(1)在![]() ,
,![]() ,
,![]() 中可以成为矩形
中可以成为矩形![]() 的“等距圆”的圆心的是__________.
的“等距圆”的圆心的是__________.
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是矩形的“等距圆”,那么点
是矩形的“等距圆”,那么点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() ,其中
,其中![]() 点坐标为
点坐标为![]() ,对称轴
,对称轴![]() 为直线
为直线![]() .
.
(1)求抛物线的解析式;
(2) 在![]() 轴上方有一点
轴上方有一点![]() , 连接
, 连接![]() 后满足
后满足![]() , 记
, 记![]() 的面积为
的面积为![]() , 求当
, 求当![]() 时点
时点![]() 的坐标
的坐标
(3)在![]() 的条件下,当点
的条件下,当点![]() 恰好落在抛物线上时,将直线
恰好落在抛物线上时,将直线![]() 上下平移,平移后的
上下平移,平移后的![]() 时点
时点![]() 的坐标;直线
的坐标;直线![]() 与抛物线交于
与抛物线交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若以点
的左侧),若以点![]() 为顶点的三角形是直角三角形,求出
为顶点的三角形是直角三角形,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织健康知识竞赛,每班参加竞赛的人数相同,成绩为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
一班竞赛成绩统计图
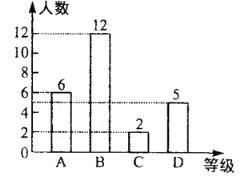
二班竞赛成绩统计图
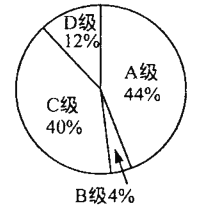
一班和二班竞赛成绩统计表(部分空缺)
成绩 班级 | 众数 | 中位数 | 优秀率 | 平均分 |
一班 | 90 |
|
| 87.6 |
二班 |
| 80 |
|
|
请根据以上图表的信息解答下列问题:
(1)求![]() ,
,![]() ,
,![]() 的值.
的值.
(2)若全校共有750名学生参加竞赛,估计成绩优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
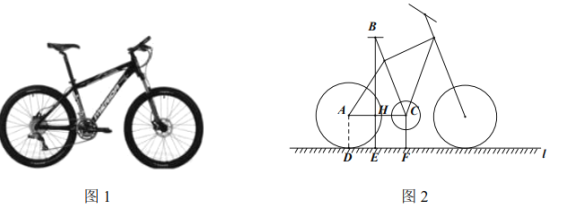
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移
的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移![]() 个单位,得到点B.
个单位,得到点B.
(1)求点B的坐标(用含b的式子表示);
(2)当抛物线经过点![]() ,且
,且![]() 时,求抛物线的表达式;
时,求抛物线的表达式;
(3)若抛物线与线段AB恰有一个公共点,结合图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
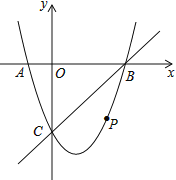
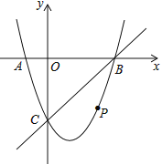
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),与
),与![]() 轴交于
轴交于![]() (
(![]() ,
,![]() ),点
),点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结![]() 、
、![]() ,并把△
,并把△![]() 沿
沿![]() 边翻折,得到四边形
边翻折,得到四边形![]() , 那么是否存在点
, 那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大并求出此时
的面积最大并求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com