
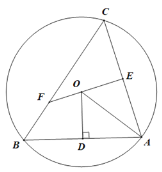
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
【答案】(1)见解析;(2)是,证明见解析.
【解析】
(1)利用圆周角定理可知∠ECF=![]() ∠AOB,再由垂径定理得到∠AOD=
∠AOB,再由垂径定理得到∠AOD=![]() ∠AOB,从而证明∠ECF=∠AOD,再由垂径定理可得∠ODA=∠CEF=90°,由此即可得出结论;
∠AOB,从而证明∠ECF=∠AOD,再由垂径定理可得∠ODA=∠CEF=90°,由此即可得出结论;
(2)由已知易证△OEC∽△CEF,从而可得∠ECF=∠EOC,再根据圆周角定理证明∠EOC=∠CBA,从而可得∠ECF=∠CBA,由等角对等边即可得出结论.
证明:(1)连接OB,
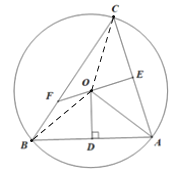
∵![]() ,
,
∴∠ECF=![]() ∠AOB,
∠AOB,
又∵OD⊥AB,OA=OB,
∴∠AOD=![]() ∠AOB,
∠AOB,
∴∠ECF=∠AOD,
∵OD⊥AB ,
∴∠ODA=90°,
∵E为AC中点 ,
∴OE⊥AC,
∴∠CEF=90°,
∴△CEF∽△ODA.
(2)∵OE·EF=CE2,∠OEC=∠CEF,
∴△OEC∽△CEF,
∴∠ECF=∠EOC,
∵∠EOC=![]() ,∠CBA=
,∠CBA=![]()
∴∠ECF=∠CBA,
∴△ABC是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
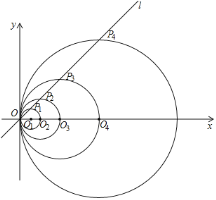
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长___________.
的长___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,探究发现规律,并解决问题,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接写出第④个等式: ;
(2)猜想第![]() 个等式(用含字母
个等式(用含字母![]() 的式子表示),并说明这个等式的正确性;
的式子表示),并说明这个等式的正确性;
(3)利用发现的规律,求![]() 的值.(参考数据:
的值.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.

(1)求抛物线的解析式.
(2)若![]() 为第二象限内一点,且四边形
为第二象限内一点,且四边形![]() 为平行四边形,求直线
为平行四边形,求直线![]() 的解析式.
的解析式.
(3)![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,∠1=40°,∠2=80°,则∠3的度数为( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/15/2485292109684736/2491850430775296/STEM/0502255e02c3498e9234cb6eaef26eb9.png]
A.120°B.130°C.140°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
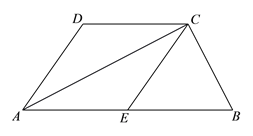
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() .折叠该纸片,使点
.折叠该纸片,使点![]() 落在线段
落在线段![]() 上,折痕与边
上,折痕与边![]() 交于点
交于点![]() ,与边
,与边![]() 交于点
交于点![]() .
.
(1)若折叠后使点![]() 与点
与点![]() 重合,此时
重合,此时![]() __________;
__________;
(2)若折叠后使点![]() 与边
与边![]() 的中点重合,求
的中点重合,求![]() 的长度;
的长度;
(3)若折叠后点![]() 落在边
落在边![]() 上的点为
上的点为![]() ,且使
,且使![]() ,求此时
,求此时![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
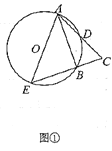
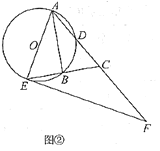
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com