
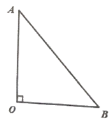
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() .折叠该纸片,使点
.折叠该纸片,使点![]() 落在线段
落在线段![]() 上,折痕与边
上,折痕与边![]() 交于点
交于点![]() ,与边
,与边![]() 交于点
交于点![]() .
.
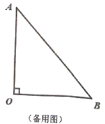
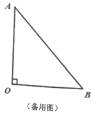
(1)若折叠后使点![]() 与点
与点![]() 重合,此时
重合,此时![]() __________;
__________;
(2)若折叠后使点![]() 与边
与边![]() 的中点重合,求
的中点重合,求![]() 的长度;
的长度;
(3)若折叠后点![]() 落在边
落在边![]() 上的点为
上的点为![]() ,且使
,且使![]() ,求此时
,求此时![]() 的长度.
的长度.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的x的取值范围
的x的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
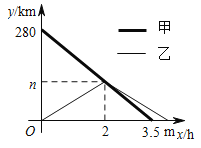
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地,甲、乙两车距
地,甲、乙两车距![]() 地的路程
地的路程![]() 与各自行驶的时间
与各自行驶的时间![]() 之间的关系如图所示.
之间的关系如图所示.
⑴![]() ________,
________,![]() ________;
________;
⑵求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当甲车到达![]() 地时,求乙车距
地时,求乙车距![]() 地的路程
地的路程
查看答案和解析>>
科目:初中数学 来源: 题型:
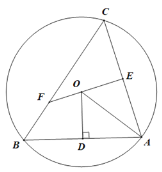
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
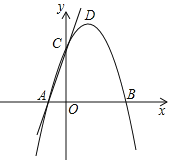
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点C,点D时抛物线的顶点
轴交于点C,点D时抛物线的顶点
(1)求抛物线的解析式和直线![]() 的解析式;
的解析式;
(2)试探究:在抛物线上是否存在点P,使得以点![]() 为顶点,
为顶点,![]() 为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
为直角边的三角形是直角三角形,若存在,请求出,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于![]() 及一个矩形给出如下定义:如果
及一个矩形给出如下定义:如果![]() 上存在到此矩形四份顶点距离都相等的点,那么称
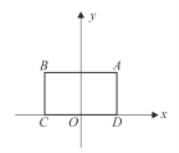
上存在到此矩形四份顶点距离都相等的点,那么称![]() 是该矩形的“等距圆”,如图,平面直角坐标系
是该矩形的“等距圆”,如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() 的半径为
的半径为![]() .
.
(1)在![]() ,
,![]() ,
,![]() 中可以成为矩形
中可以成为矩形![]() 的“等距圆”的圆心的是__________.
的“等距圆”的圆心的是__________.
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是矩形的“等距圆”,那么点
是矩形的“等距圆”,那么点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
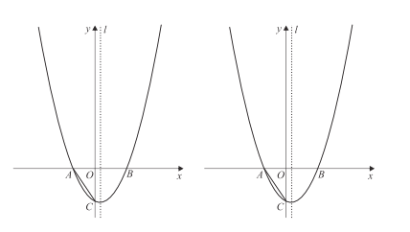
【题目】如图,已知抛物![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() ,其中
,其中![]() 点坐标为
点坐标为![]() ,对称轴
,对称轴![]() 为直线
为直线![]() .
.
(1)求抛物线的解析式;
(2) 在![]() 轴上方有一点
轴上方有一点![]() , 连接
, 连接![]() 后满足
后满足![]() , 记
, 记![]() 的面积为
的面积为![]() , 求当
, 求当![]() 时点
时点![]() 的坐标
的坐标
(3)在![]() 的条件下,当点
的条件下,当点![]() 恰好落在抛物线上时,将直线
恰好落在抛物线上时,将直线![]() 上下平移,平移后的
上下平移,平移后的![]() 时点
时点![]() 的坐标;直线
的坐标;直线![]() 与抛物线交于
与抛物线交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若以点
的左侧),若以点![]() 为顶点的三角形是直角三角形,求出
为顶点的三角形是直角三角形,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
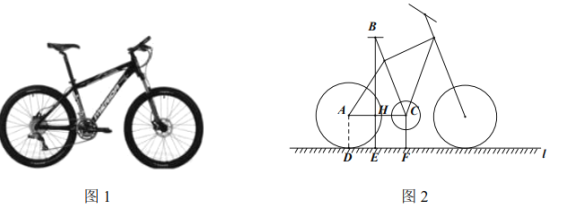
查看答案和解析>>
科目:初中数学 来源: 题型:
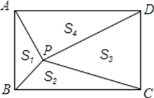
【题目】如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断,其中不正确的是( )
A.PA+PB+PC+PD的最小值为10
B.若△PAB≌△PCD,则△PAD≌△PBC
C.若△PAB△PDA,则PA=2
D.若S1=S2,则S3=S4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com