
【题目】观察下列等式,探究发现规律,并解决问题,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接写出第④个等式: ;
(2)猜想第![]() 个等式(用含字母
个等式(用含字母![]() 的式子表示),并说明这个等式的正确性;
的式子表示),并说明这个等式的正确性;
(3)利用发现的规律,求![]() 的值.(参考数据:
的值.(参考数据:![]() )
)
【答案】(1)35﹣34=2×34;(2)猜想:第n个等式为:3n+1﹣3n=2×3n.理由见解析;(3)88572
【解析】
(1)根据已知规律写出④即可.
(2)根据已知规律写出n个等式,利用提公因式法即可证明规律的正确性.
(3)根据发现的规律得到(32-31)+(33-32)+(34-33)+…+(311-310)=2(31+32+33+…+310),依此可求31+32+33+…+310的值.
(1)①![]() ;
;
②![]() ;
;
③![]() ;
;
∴第④个等式:35-34=2×34;
故答案为:35-34=2×34;
(2)猜想:第n个等式为:3n+1﹣3n=2×3n.
理由如下:
∵3n+1﹣3n=3×3n﹣3n=(3﹣1)×3n=2×3n,
∴3n+1﹣3n=2×3n;
(3)根据发现的规律,有:311﹣310=2×310,
∴(32﹣31)+(33﹣32)+(34﹣33)+…+(311﹣310)=2(31+32+33+…+310),
∴311﹣31=2(31+32+33+…+310),
即31+32+33+…+310=![]() (311﹣3).
(311﹣3).
∵311=177147,
∴31+32+33+…+310=![]() (177147﹣3)=88572.
(177147﹣3)=88572.


科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的x的取值范围
的x的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线的函数表达式和直线![]() 的解析式;
的解析式;
(2)若点![]() 在第二象限内,且
在第二象限内,且![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,若![]() 为直线
为直线![]() 上一点,是否存在点
上一点,是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
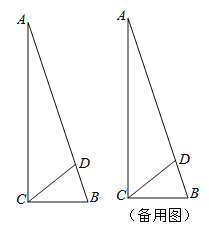
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边上一点,且
是斜边上一点,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的
的![]() 与边
与边![]() 相切,切点为
相切,切点为![]() 的中点
的中点![]() ,
,![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
(i)求![]() 的半径;
的半径;
(ⅱ)连接![]() ,试探究
,试探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
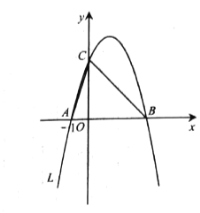
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]()
![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)![]() 与
与![]() 之间的关系式为: ;
之间的关系式为: ;
(2)判断线段![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)设点![]() 是抛物线
是抛物线![]() 上
上![]() 、
、![]() 之间的动点,连接
之间的动点,连接![]() ,
,![]() ,当
,当![]() 时:
时:
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() ,且
,且![]() 的最大值为
的最大值为![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
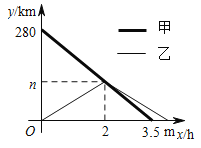
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地,甲、乙两车距
地,甲、乙两车距![]() 地的路程
地的路程![]() 与各自行驶的时间
与各自行驶的时间![]() 之间的关系如图所示.
之间的关系如图所示.
⑴![]() ________,
________,![]() ________;
________;
⑵求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当甲车到达![]() 地时,求乙车距
地时,求乙车距![]() 地的路程
地的路程
查看答案和解析>>
科目:初中数学 来源: 题型:
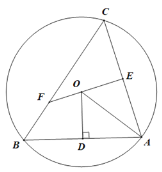
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
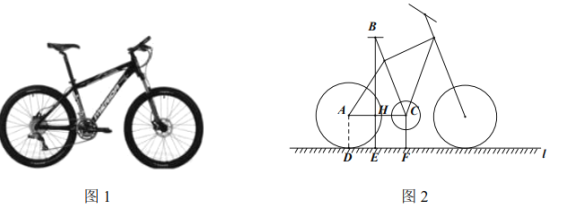
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com