
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]()
![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)![]() 与
与![]() 之间的关系式为: ;
之间的关系式为: ;
(2)判断线段![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
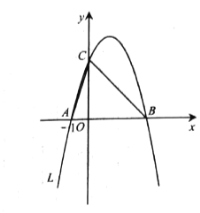
(3)设点![]() 是抛物线
是抛物线![]() 上
上![]() 、
、![]() 之间的动点,连接
之间的动点,连接![]() ,
,![]() ,当
,当![]() 时:
时:
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() ,且
,且![]() 的最大值为
的最大值为![]() ,请直接写出
,请直接写出![]() 的值.
的值.

【答案】(1)c﹣b= 1;(2)OB=OC,理由见解析;(3)①点P的坐标为(1,4)或(2,3);② ![]() 或
或![]()
【解析】
(1)将A(-1,0)代入抛物线![]() 即可得解;
即可得解;
(2)由抛物线![]() 可得点C的坐标,故可得OC=c,
可得点C的坐标,故可得OC=c,![]() 代入抛物线
代入抛物线![]() 得
得![]() 可得B(0,c),故可得OB=c,故可得结论;
可得B(0,c),故可得OB=c,故可得结论;
(3)①设点P(x,y),根据![]() 可得
可得![]() ,求解方程即可得到解答;
,求解方程即可得到解答;
②根据二次函数图象的增减性结合![]() 的最大值分3种情况求解即可.
的最大值分3种情况求解即可.
(1)∵抛物线![]() 经过
经过![]()
代入得:![]()
![]()
![]()
故答案为:![]() .
.
(2)OB=OC.
∵抛物线![]() 与
与![]() 轴交于点C,
轴交于点C,
![]()
![]()
由(1)知,![]() 代入抛物线
代入抛物线![]() 得,
得,
![]()
解得:![]() ,
,![]() ,
,
∵![]() ,
,
![]()
![]()
![]()
(3)① 当m=3时,得:![]() 解得:
解得:![]()
∴![]() .
.
∴OB=OC=3,
∵A(﹣1,0),
∴AB=4.
∴![]() .
.
连接OP(如图所示),则有:
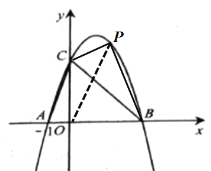
![]() .
.
∵点P(x,y)在抛物线L上,
∴![]() .
.
∴![]() ,
,
∵S△PBC=![]() S△ABC,
S△ABC,
∴![]() ,
,
即![]() ,
,
解得:x1=1,x2=2.
当x=1时,![]() ;当x=2时,
;当x=2时,![]() .
.
∴点P的坐标为(1,4)或(2,3).
②∵抛物线![]()
∴对称轴为![]()
∵图象开口向下,
![]() 时,y随x的增大而增大,
时,y随x的增大而增大,![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
a.当![]() 时,即
时,即![]() 时,y最大值
时,y最大值![]()
![]() 或
或![]() (不符合题意,舍去)
(不符合题意,舍去)
b.当![]() 时,y最大值
时,y最大值![]()
![]() (不符合题意,舍去)
(不符合题意,舍去)
c.当![]() 时,y最大值
时,y最大值![]() ,
,
![]() 或
或![]() (不符合题意,舍去)
(不符合题意,舍去)
综上所述:![]() 或
或![]()


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】我国青少年的视力情况已受到全社会的广泛关注,某校随机调研了200名初中七、八、九年级学生的视力情况,并把调查数据绘制成以下统计图:
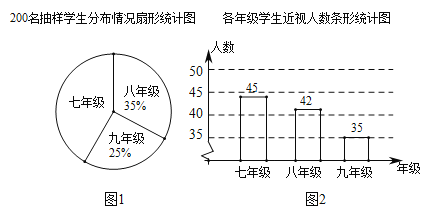
(1)七年级参加调查的有多少人?若该校有七年级学生500人,请估计七年级的近视人数;
(2)某同学说:“由图2可知,从七年级到九年级近视率越来越低.”你认为这种说法正确吗?请做判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示对于此抛物线有如下四个结论:①
,其部分图象如图所示对于此抛物线有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 若,则
若,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值其中正确结论的个数是( )
时的函数值其中正确结论的个数是( )
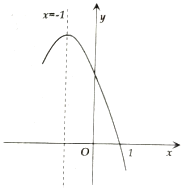
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,探究发现规律,并解决问题,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接写出第④个等式: ;
(2)猜想第![]() 个等式(用含字母
个等式(用含字母![]() 的式子表示),并说明这个等式的正确性;
的式子表示),并说明这个等式的正确性;
(3)利用发现的规律,求![]() 的值.(参考数据:
的值.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.

(1)求抛物线的解析式.
(2)若![]() 为第二象限内一点,且四边形
为第二象限内一点,且四边形![]() 为平行四边形,求直线
为平行四边形,求直线![]() 的解析式.
的解析式.
(3)![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
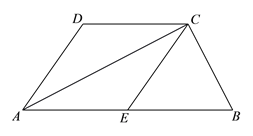
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
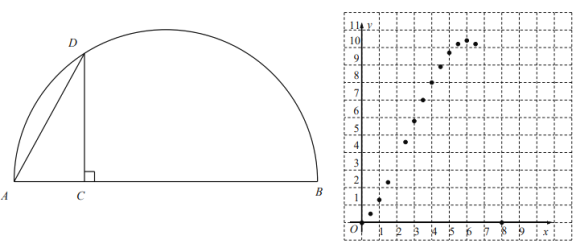
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com