
【题目】如图,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线的函数表达式和直线![]() 的解析式;
的解析式;
(2)若点![]() 在第二象限内,且
在第二象限内,且![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,若![]() 为直线
为直线![]() 上一点,是否存在点
上一点,是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]()
![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)
![]()
![]()
![]()
【解析】
(1)点A(2,0)、点B(-4,0),则函数的表达式为:y=a(x-2)(x+4),即可求解;把![]() 坐标代入
坐标代入![]() ,求出
,求出![]() 即可得出答案;
即可得出答案;
(2)PE=![]() OD,则PE=(
OD,则PE=(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)=
x+2)=![]() (-x),求得:点D(-5,0),利用S△PBE=
(-x),求得:点D(-5,0),利用S△PBE=![]() PE×BD=
PE×BD=![]() (
(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)(-4-x),即可求解;
x+2)(-4-x),即可求解;
(3)分三种情况求解即可:①当BD=BM时,②当BD=DM时,③当BM=DM时.
(1)经过![]() ,对称轴
,对称轴![]() ,
,
![]()
设解析式为![]() ,
,
![]() ,
,
∴﹣8a=﹣2
![]()
![]()
=![]()
设直线![]() ,经过
,经过![]()
![]() ..
..
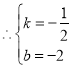
![]()
(2)设![]() ,则
,则![]()
![]()
![]()
![]() 或
或![]() .(舍)
.(舍)
![]()
=![]()
=![]()
=![]()
(3)∵直线![]() ,
,![]()
∴设M(m,![]() )
)
∵B(-4,0),D(-5,0),M(m,![]() )
)
∴![]()


当BD=BM时,即![]()
∴![]()
∴![]()
∴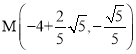 或
或
当BM=DM时,![]()
∴![]()
∴![]()
∴![]()
当BD=DM时,![]()
∴![]()
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()
故答案为: ,
,![]() ,
,![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
小明将两个全等的![]() 和
和![]() 重叠在一起,其中
重叠在一起,其中![]() ,
,![]() ,
,![]() . 固定△DEF不动,将△ABC沿直线ED向左平移,当B与D重合时停止移动.
. 固定△DEF不动,将△ABC沿直线ED向左平移,当B与D重合时停止移动.
猜想证明:
(1)如图1,在平移过程中,当点D为AB中点时,连接DC,CF,BF,请你猜想四边形CDBF的形状,并证明你的结论;

(2)如图2,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断地变化,判断它的面积变化情况,并求出其面积;
探索发现:
(3)在平移过程中,四边形CDBF有什么共同特征?(写出两个即可)________,________;
(4)请你提出一个与△ABC平移过程有关的新的数学问题(不必证明和解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
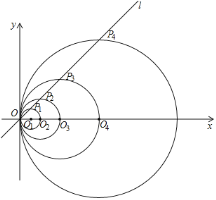
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长___________.
的长___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
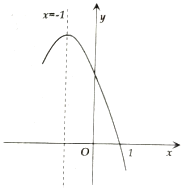
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,其部分图象如图所示对于此抛物线有如下四个结论:①
,其部分图象如图所示对于此抛物线有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 若,则
若,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值其中正确结论的个数是( )
时的函数值其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,探究发现规律,并解决问题,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接写出第④个等式: ;
(2)猜想第![]() 个等式(用含字母
个等式(用含字母![]() 的式子表示),并说明这个等式的正确性;
的式子表示),并说明这个等式的正确性;
(3)利用发现的规律,求![]() 的值.(参考数据:
的值.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.

(1)求抛物线的解析式.
(2)若![]() 为第二象限内一点,且四边形
为第二象限内一点,且四边形![]() 为平行四边形,求直线
为平行四边形,求直线![]() 的解析式.
的解析式.
(3)![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
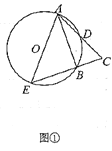
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
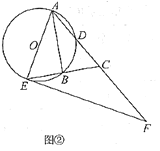
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com