
【题目】在平面直角坐标系xOy中,抛物线![]() 的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移
的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移![]() 个单位,得到点B.
个单位,得到点B.
(1)求点B的坐标(用含b的式子表示);
(2)当抛物线经过点![]() ,且
,且![]() 时,求抛物线的表达式;
时,求抛物线的表达式;
(3)若抛物线与线段AB恰有一个公共点,结合图象,直接写出b的取值范围.
【答案】(1)(0,3-b2);(2)![]() ;(3)-1≤b≤1
;(3)-1≤b≤1
【解析】
(1)先求出点A坐标,再根据平移规律即可求出点B坐标;
(2)把(0,2)代入![]() ,结合b>0即可求出b,问题得解;
,结合b>0即可求出b,问题得解;
(3)把B坐标代入抛物线解析式,求出b,分b>1,b=1,-1<b<1,b=-1,b<-1,画出函数图象,即可求解.
解:(1)由题意得抛物线![]() 的对称轴为
的对称轴为![]() ,
,
∴点A坐标为(b,0),
∴点B坐标为(0,3-b2)
(2)把(0,2)代入![]() 中,
中,
解得b=±1.
∵b>0,
∴b=1.
∴抛物线的表达式:![]() ;
;
(3)当抛物线过点B时,抛物线AB有一个公共点,
∴![]()
∴![]() ,
,
如图:当b>1时,抛物线与线段AB无交点;
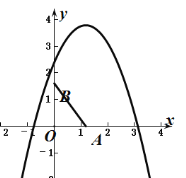
当b=1时,抛物线与线段AB有一个交点;
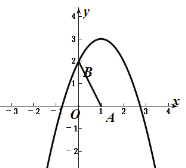
当-1<b<1时,抛物线与线段AB有一个交点;
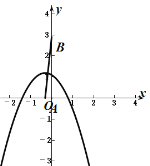
当b=-1时,抛物线与线段AB有一个交点;
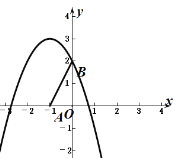
当b<-1时,抛物线与线段AB无交点.
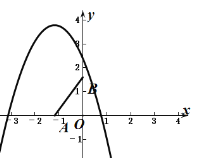
∴若抛物线与线段AB恰有一个公共点,则-1≤b≤1.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.

(1)求抛物线的解析式.
(2)若![]() 为第二象限内一点,且四边形
为第二象限内一点,且四边形![]() 为平行四边形,求直线
为平行四边形,求直线![]() 的解析式.
的解析式.
(3)![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
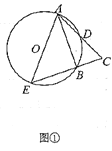
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
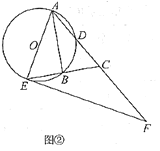
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
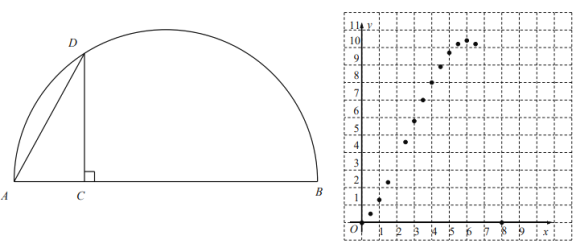
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,AC为一条对角线,且![]() .延长BC到点E,使
.延长BC到点E,使![]() ,连接DE.
,连接DE.
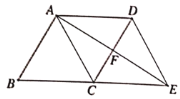
(1)判断四边形ACED的形状,并说明理由;
(2)连接AE交CD于点F,若![]() ,
,![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
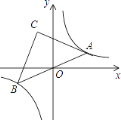
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
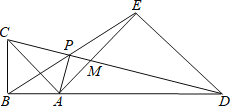
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】速滑运动受到许多年轻人的喜爱,如图,梯形BCDG是某速滑场馆建造的速滑台,已知CD∥EG,高DG为4米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为1:![]() .
.
(1)求新坡面AC的坡角;
(2)原坡面底部BG的正前方10米(EB的长)处是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由.(参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com